作者:實作派
接觸過電磁學的人應該有看過史密斯圖 Smith Chart ,它是設計微波電路的好幫手,雖然現今有各種 CAD 軟體輔助設計,但在阻抗匹配上面的理解與視覺呈現上,Smith Chart 絕對是勝出的,無人能出其右。
本篇文章針對 Smith Chart 與傳輸線做摘要式的總覽,重點會放在 Smith Chart 的基本使用方式。我並不打算說明 Smith Chart 如何產生,因為這會牽扯到傳輸線理論,那可是會有一長串的公式導證過程,而這段過程的細節在所有的電磁學課本內都有,大家自己看書就可以。
傳輸線 Transmission Line
我們一般常用的有線電視電纜線或是 Wifi 機器內連接用的訊號線,都屬於傳輸線的一種,甚至 PCB 上面的 trace 線也是傳輸線;當頻率越來越高,波長越來越短時,我們就必須以傳輸線模型來考慮訊號的傳遞了。
例如當訊號頻率在 100 MHz 時,波長有 3 公尺,但如果是 Wifi 訊號的 5 GHz 頻段,波長就只剩 6 公分,在這個時候,因為波長很短,甚至短過 PCB 板的尺寸,表示在同一個瞬間,在 PCB 導線上的不同位置會出現不同的電壓電流,因此需要不同的思維來考慮電路,也就是傳輸線理論的價值所在。
由於波長短的緣故,在高頻電路的設計上,傳輸線的長度、元件尺寸、介電常數等都須納入考慮,這與以往的電路考量是非常不同的。
下圖兩條金屬線就是很典型的傳輸線,末端再放個負載 ZL,接著就可以探討電波輸入端的阻抗,光是這樣就可以算到昏天暗地了,後面我會說明如何利用 Smith Chart 簡化計算,當然用 CAD 軟體會更迅速,但我們還是得學點前人的真功夫,畢竟 Smith Chart 還是相當視覺化的,很方便用來溝通。
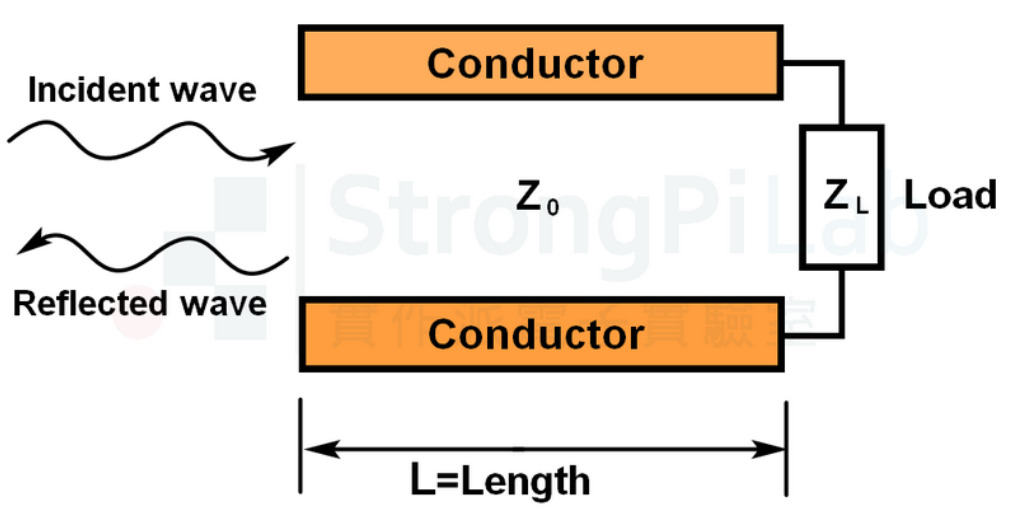
(圖片來源:實作派提供)
上面傳輸線的輸入端反射率,經過一連串複雜的計算之後,公式如下:
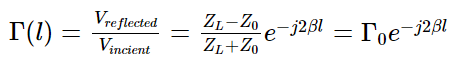
(圖片來源:實作派提供)
ZL 是負載阻抗、Z0是特徵阻抗、ι 是傳輸線長度,至於 β 則是角波數,它的概念與時域的角頻率 ω 是一樣的,但頻率這個詞已經被時域用掉了,所以電壓在空間距離上的變化我們稱為波數,詳情可以參考【實作實驗室】波長與週期誰是誰,別再搞混了!。β 與 Z0 是材料特性,不同材料會有不同的值。
如果傳輸線的特徵阻抗 Z0 與負載阻抗 ZL 不同,反射率不為零,表示阻抗不匹配,此時入射波就會發生反射,你可以回想在透明玻璃上仍會隱約看到自己的影像,這是一樣的道理,因為玻璃與空氣的介質不同,造成部分光線反射。
若訊號傳輸過程中有發生反射,等於自己干擾自己,這時就需要在傳輸線上做些改變,甚至加上一些元件來讓反射變小,這個過程稱為「阻抗匹配」,但無論是改導線長度還是加元件,PCB 板都已經洗好固定了,要怎麼改?這時就只有花錢再做一塊板子囉!這就是為什麼老經驗的射頻工程師較有價值的原故,因為他可以幫老闆省下開發費用,當然這種人相對來說也較為不善言辭,常常讓老闆又愛又恨。
你可能有發現為何反射率公式裡面會有虛數?那是因為當初求解傳輸線波動微分方程式的時候,是以複數型式的訊號 V(x)ejwt 代進去求解,所以算出來的反射率也會有虛數出現,這個虛部可以反映電波的相位差,這通常是電容或電感效應造成的,各位可以參考【實作實驗室】一次搞懂虛功率、實功率、視在功率與功率因數,雖然講的是電力系統,但是儲能元件造成相位差的道理是一樣的。
特徵阻抗
傳輸線圖中的 Z0 稱為特徵阻抗,屬於材料特性,我們一般在外面買的同軸電纜線有分為 50 ohm/75 ohm 指的就是特徵阻抗,特徵阻抗並不是導線電阻,我還特別寫了一篇來講這件事,請看這篇阻抗 75 ohm 的同軸 Cable 與 75 ohm 的電阻-兩者別搞混。
下圖是一條名為 LMR-400 的 50 ohm 電纜線,它的官方資料很詳細,連單位長度的電容電感值都有標示出來,如黃色框框所示,我們就來驗算看看它的值合不合理。
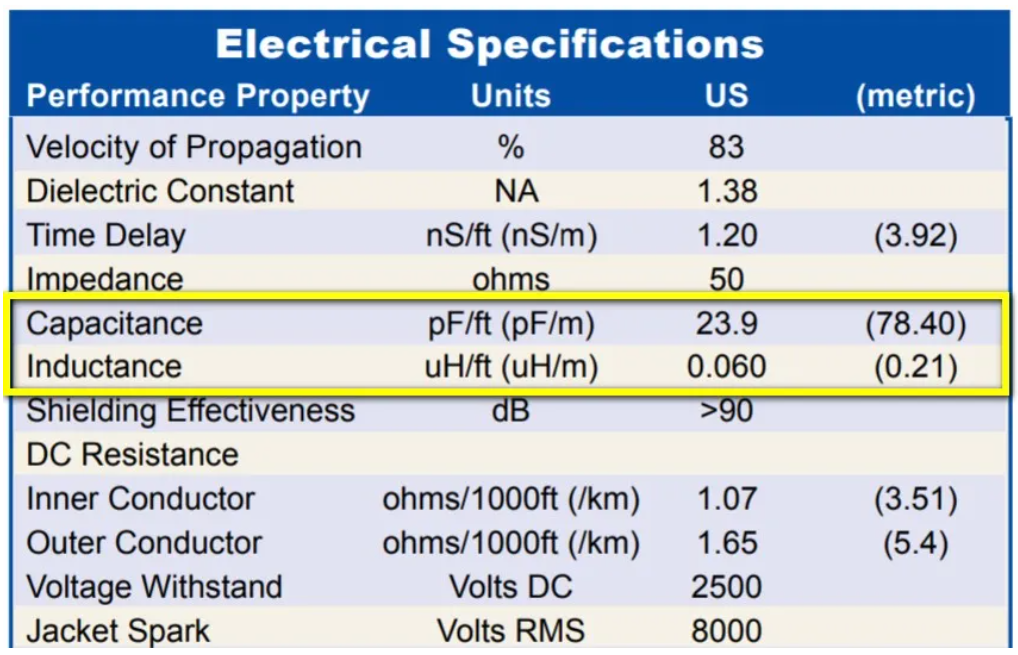
LMR-400 cable spec(圖片來源:實作派提供)
根據電磁學理論,在低耗損的傳輸線中,特徵阻抗的公式如下:
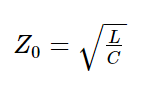
(圖片來源:實作派提供)
然後把黃色方框內的電感值與電容值代入公式中,就可以得到特徵阻抗是 51.75 ohm。咦!為什麼不是剛好 50 ohm?因為這是現實世界,可能是當時取樣有誤差、Cable 生產時有誤差,也可能是原廠當時測試的時候,儀器本身的誤差,總之它一定不會剛好是 50 ohm,但會是個很接近 50 ohm 的值。
我想這些 Cable 大廠都會自己做規格的抽樣檢驗,畢竟我們會驗算的東西,原廠一定自己也算過,但話說回來,紙上的資料畢竟只是參考而已,如果要真正驗證手頭上的 Cable 是不是 50 ohm,省錢一點的作法是你可以利用 50 ohm 的終端電阻測試看看是否有反射波,這部分請參考 同軸電纜壓接頭檢測-利用反射波一翻兩瞪眼 ,高階一點的測法可能就需要網路分析儀了。
導線長度與反射率
剛剛的反射率公式包含了一個歐拉公式 e−j2βl,歐拉公式本身在複數平面上是以一個單位圓來呈現,它的次方項有個導線長度 ι,如果導線長度變長的話,反映在複數平面的變化就會是,以圓點為中心,由目前的反射率順時針行走的變化,你可以將它視為下圖的極座標表示型式 Γ=Γ0∠(−j2βl)。
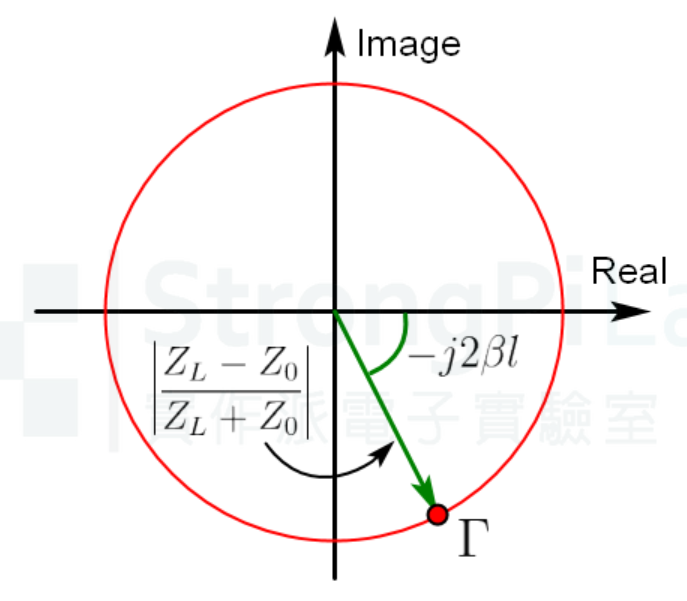
反射率在複數平面的極座標形式(圖片來源:實作派提供)
當然,要看到這種變化,前提是反射率必須不為零,這樣才有半徑可言,這個半徑就是 ,半徑不為零,Γ0才能夠轉圈圈,我們才能看得到反射率變化;如果反射率等於零,半徑也等於零,不管導線多長多短,反射率全都只會是一個中心點。
關於這個半徑的範圍我們來推論一下,由於負載阻抗 ZL 會介於短路 Short 與開路 Open 之間,所以 ZL 的值會介於 0∼∞ 之間,因此 Γ0 的值會介於 -1 和 1 之間。
以下就是負載阻抗 ZL 與特徵阻抗 Z0 在三種特別情況的時候,反射率的振幅會呈現甚麼狀況:
- Γ0=−1 表示負載短路 Short
- Γ0=0 表示負載阻抗匹配 Impedance Match,無反射
- Γ0=1 表示負載開路
所以不管你怎麼算,反射率 Γ 一定只存在於半徑 Γ0 的圓內,這個圓就是將來 Smith Chart 的外框。
反射率的功能
你一定有發現負載短路時的半徑 Γ0 怪怪的,它可以是負數嗎?可以,那就視為正半徑繞了 180 度,但就物理上來說這又是什麼意思呢?
如果反射率的半徑 Γ0 是正數,表示反射波會同相位反射回來;若 Γ0 是負數,表示反射波會反相位反射回來,這部分我在時域上有做過實驗,各位可以參考同軸電纜壓接頭檢測-利用反射波一翻兩瞪眼的後半段,如果你用繩子綁牆壁來做實驗也會得到相同結果。
為何反射率在高頻電路中的地位舉足輕重?因為它與大部分的參數有關係,可以有見微知著的效果。
透過反射率 Γ 在複數平面的位置,我們就可以視覺化的知道,現在的反射率是多少。前面有提到反射率外圈的最左邊與最右邊,可以表示負載的 Short(阻抗為零)與 Open(阻抗無窮大),那是否意味著其實反射率的這個圈圈內的任一點,與負載阻抗有某種關係?答案是肯定的,這個反射率的圓圈內,只要再加上相對應的阻抗,就能做到反射率與阻抗可以利用視覺來運算,所以 Smith Chart 就此誕生。
反射率怎麼測量
反射率又稱為 S11 參數,它是 S 參數的其中一個,導證過程也是很繁雜,這裡就先不介紹 S 參數的細節, S11 的量需要靠網路分析儀 Network Analyzer,它能同時發射與接收訊號,才有辦法測量入射波與反射波。
你一定覺得奇怪,測試反射率的儀器為何會稱為「網路」分析儀,那是因為在電子電路裡面,每個由元件兜出來的小電流迴路,稱為 Mesh,很多 mesh 湊起來就變成一個 Network,這跟現今 TCP/IP 網路世界的 Network 是不同的。
Smith Chart 史密斯圖
下面這張看起來像貝殼的圖,就是史密斯圖 Smith Chart。它的特色就是在反射率的複數平面上,順便也把輸入阻抗的實部與虛部標示上去,也就是說 Smith Chart 連結了反射率與輸入阻抗,於是瞬間我們就可以直接從圖上快速地在輸入阻抗與反射率之間做轉換。我認為這是劃時代的發明,即便是現在科技如此發達,在反射與阻抗的呈現上,Smart Chart 仍然佔有一席之地。
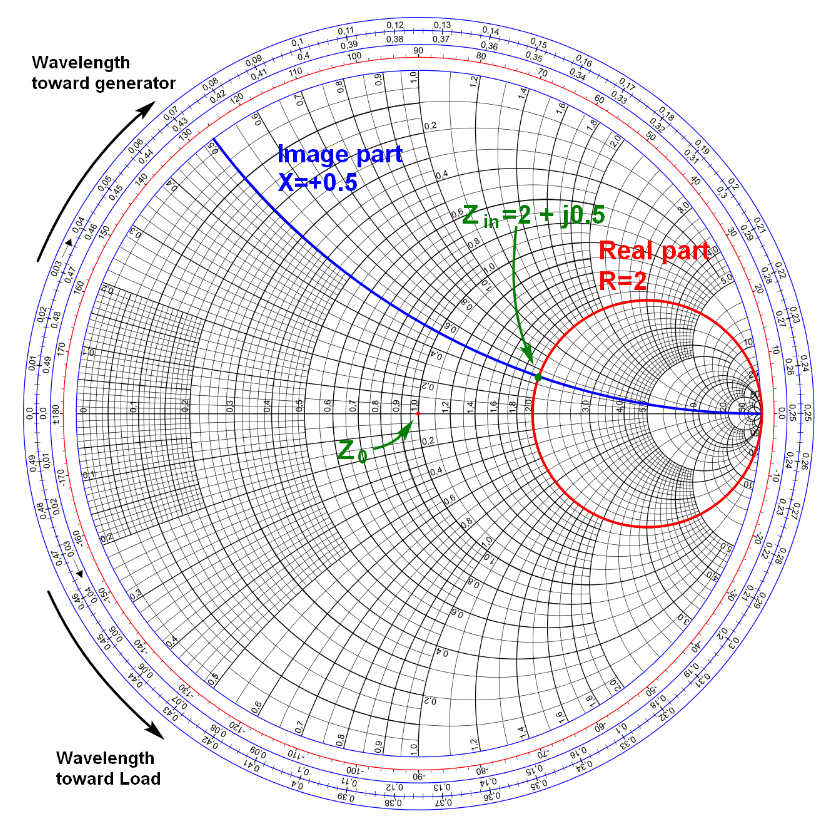
史密斯圖 Smith Chart 正規化版本(圖片來源:實作派提供)
來個實際使用 Smith Chart 的例子,讓你知道它多好用。根據前面傳輸線的電路,假設負載 ZL=100+j25.5 ,特徵阻抗 Z0=50,那麼入射端的反射率應該是多少?
基本上只要找到對應阻抗的實部與虛部,就可以作答了,但是上圖中的實部 R 為何是 2 而不是 100?因為上圖是正規化版本的 Smith Chart,它會把所有的阻抗都先除以 Z0,或是說以 Z0 為基準後,再來看反射率,這樣不會影響反射率的結果,好處是在任何阻抗系統都可以使用這張圖表,這樣就不用印好幾種版本。
回到剛剛的例子,原本的 ZL=100+j25.5,正規化之後就會變成 ZL=R+jX=2+j0.5,在上圖中所有緊靠右邊的圓都是阻抗的實部,於是我們找到 R=2 這個圓,接著找到從右邊發散的放射狀曲線,這些表示阻抗的虛部,於是再找到 X=0.5 的曲線,最後在 R 圓與 X 曲線的交會處,就是我們要找的輸入阻抗,而且還可以得出反射率大約是 0.37∠17.3∘。
實際阻抗的 Smith Chart
雖然正規化的 Smith Chart 看來很萬能,但我個人較偏好以實際特徵阻抗標示的圖,因為這樣就不需要再把特徵阻抗乘回來,多做一次計算,以前是因為一張 Smith Chart 的圖紙,要給所有的特徵阻抗用,所以需要正規化。現在有電腦輔助工具了,要什麼阻抗都有,所以我就偏好使用實際阻抗的圖。
快速計算導納
在做阻抗並聯計算的時候,把阻抗改用導納來處理會比較方便,因為這樣會變成單純的加法,但如何利用 Smith Chart 快速計算導納呢?拿 ZL=25+j25 當作範例,若需要計算導納 Y 的話,只需要把 Smith Chart 轉 180 度,就能輕易得知。
導納是阻抗的導數,單位為姆歐 Mho(Ω−1),後來這個單位統稱為西門子 S:
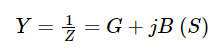
(圖片來源:實作派提供)
下圖的左方有一個重疊的 Smith Chart,它就是轉 180 度之後的圖,所以同一個點的 ZL=25+j25 只需要觀看旋轉之後的圖,就能知道 Y=20m−j20m,光用眼睛看就知道導納值,這真是很酷的工具。
阻抗與導納合併的 Smith Chart 50 ohm 版本(圖片來源:實作派提供)
傳輸線長度
若負載阻抗不是剛好 50 ohm 的話,那麼傳輸線長度的增減會改變反射率,由於反射率的公式當初在推導的時候,是以負載端當作長度為零,因此傳輸線長度增長的話,表示長度是往訊號源延伸,而阻抗點會順時針旋轉,轉一圈是 1/2 個波長,轉半圈是 1/4 波長。
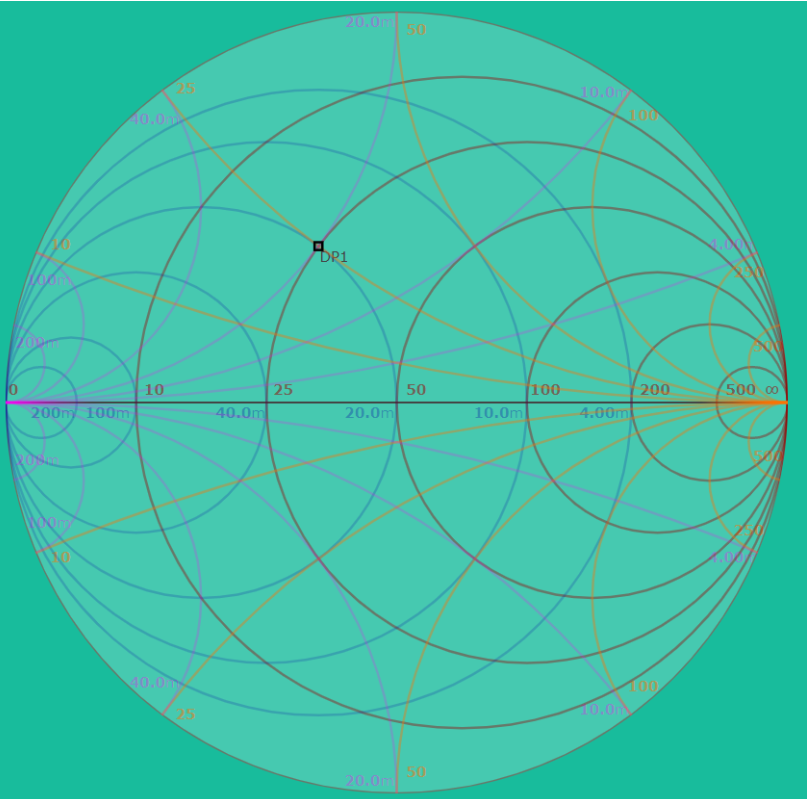
假設負載是 50+j50 ohm 如下圖的 DP1,工作頻率為 2.4G Hz,此時波長為 125 mm,若傳輸線長度為 30 mm,那麼隨著傳輸線長度增加,輸入阻抗會順時針繞大約 1/4 個波長來到 DP2 也就是 26.7-j28.2 ohm。
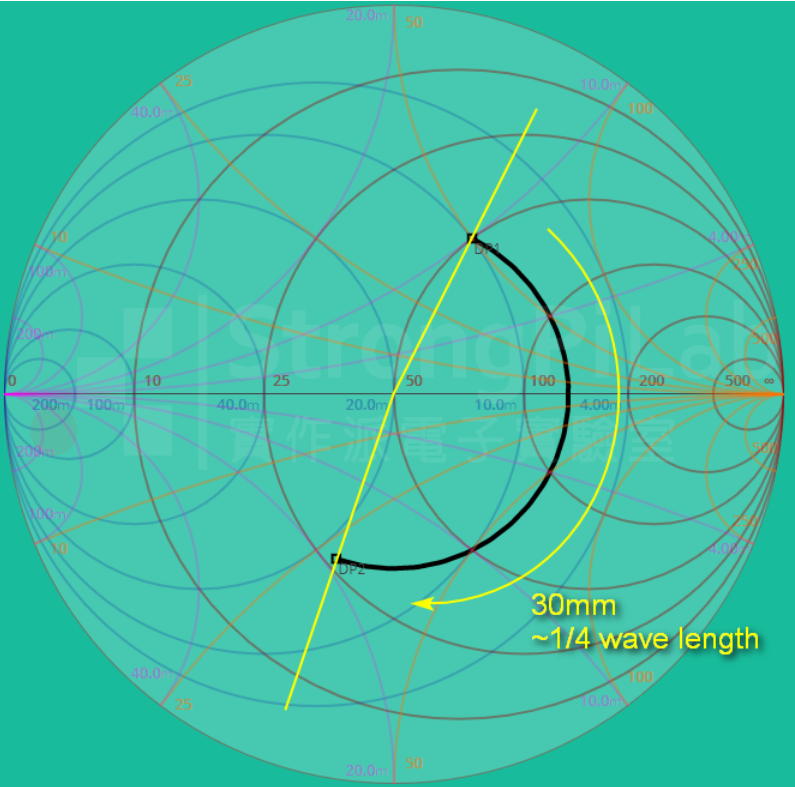
傳輸線長度增加會讓反射率順時針旋轉(圖片來源:實作派提供)
阻抗匹配
接著就來試著利用 Smith Chart 做阻抗匹配,假設電路要工作在 4G Hz,負載阻抗為 25+j10 ohm,該怎麼做才會讓輸入端變成 50 ohm呢?我的做法是先拉一條 23 mm 長的傳輸線,再串一個 1.5 nH 的電感,就能達成阻抗匹配,如下圖。
注意這張圖的負載在左邊,輸入阻抗在右邊。
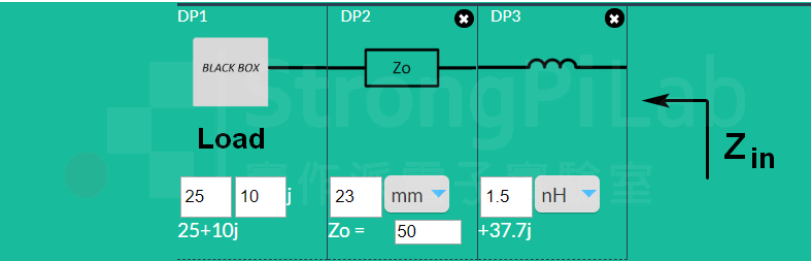
阻抗匹配線路(圖片來源:實作派提供)
整個過程其實看下圖 Smith Chart 上的軌跡就知道為什麼要這樣配,先看負載點 DP1,它的位置在 25 ohm 的圓上,我想把它弄到 50 ohm 的圓上,所以我利用加長傳輸線距離,讓反射率以圓點為中心順時針繞到 DP2,至於這個傳輸線的距離是 try 出來的,我在軟體上對長度加加減減,結果是 23 mm 的長度會讓阻抗落在 50 ohm 的圓上面。
接下來就要想辦法讓反射率落在原點,既然目標中心點已經是在 DP2 實部圓的順時針方向,我就採用串聯電感來達成,因為串電感會讓虛部增加,所以也是慢慢 try,刻意讓 DP3 落在反射率的原點,也就是阻抗 50+j0 ohm 的點,這樣就達成匹配了。
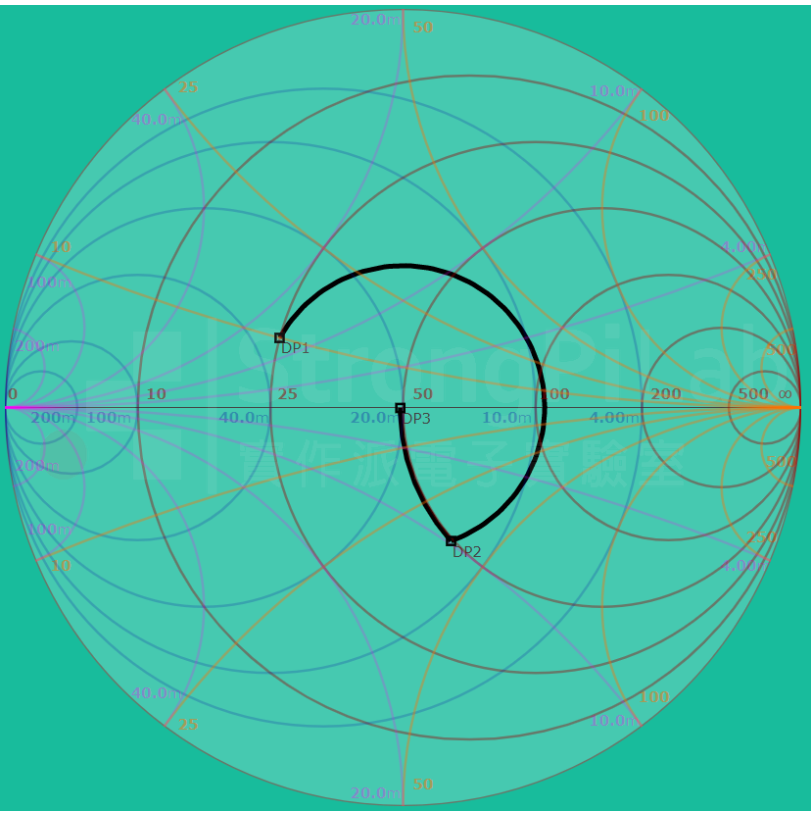
在 Smith Chart 做阻抗匹配(圖片來源:實作派提供)
雖然剛剛的阻抗已經做好匹配,但你要知道那只在 4G Hz 的時候匹配,隨著頻率變高或變低,波長也會改變,這表示剛剛傳輸線選的 23 mm 長度,在其他頻率就不再適用了,那所謂不適用到底是差多少呢?
我們把頻率範圍從 2G Hz 開到 6 GHz,你就可以在下圖看到一條紅色的軌跡,這就是傳輸線的頻率響應 Frequency Response,頻率響應這件事情目前只有模擬軟體能做,單看 Smith Chart 做不到,因為這需要類似 Spice 這種功能。
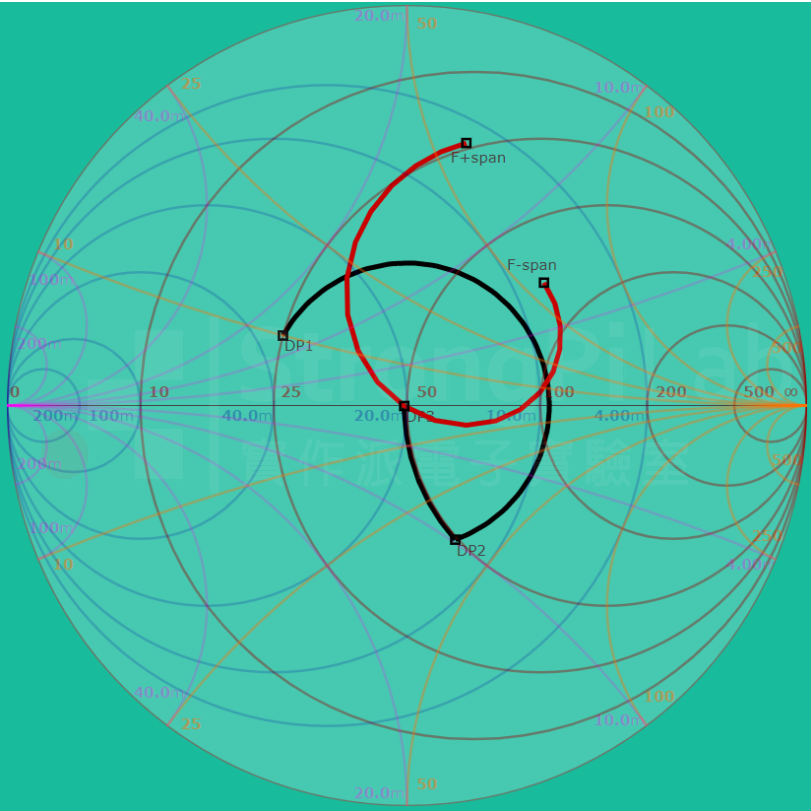
在 Smith Chart 上的頻率響應(圖片來源:實作派提供)
上圖的 F-span 就是 2G Hz,F+span 就是 6G Hz,你會發現越靠近 4G Hz 就越靠近中心的匹配點,頻率越遠,輸入阻抗早已不知飄到哪裡去了,所以其實窄頻通訊比較好設計,寬頻通訊要顧慮的面向較多,相對比較困難。
希望這篇文章可以讓各位理解 Smith Chart 的基本用法,關於利用網路分析儀測試同軸電纜的理論與實務差異,請看 反射率 S11 實測-同軸電纜/終端電阻 在 Smith Chart 長甚麼樣子 。
(本文經同意轉載自實作派電子實驗室、原文連結;責任編輯:賴佩萱)
- 【實作實驗室】分配器效能測試 - 2024/12/30
- 【實作實驗室】頻道功率怎麼測?有線電視頻譜長這樣! - 2024/12/12
- 【實作實驗室】無線滑鼠游標定格,電源開關更換 DIY - 2024/11/12
訂閱MakerPRO知識充電報
與40000位開發者一同掌握科技創新的技術資訊!



