【實作實驗室】波長與週期誰是誰，別再搞混了！

作者：實作派

先來問大家一個問題，下面有兩張圖，一張是示波器的波形，一張是水波紋，兩個波的波峰間隔姑且稱為 b，試問哪個是週期？哪個是波長？這個問題看來很容易，但卻考驗著自己的觀念是否正確。

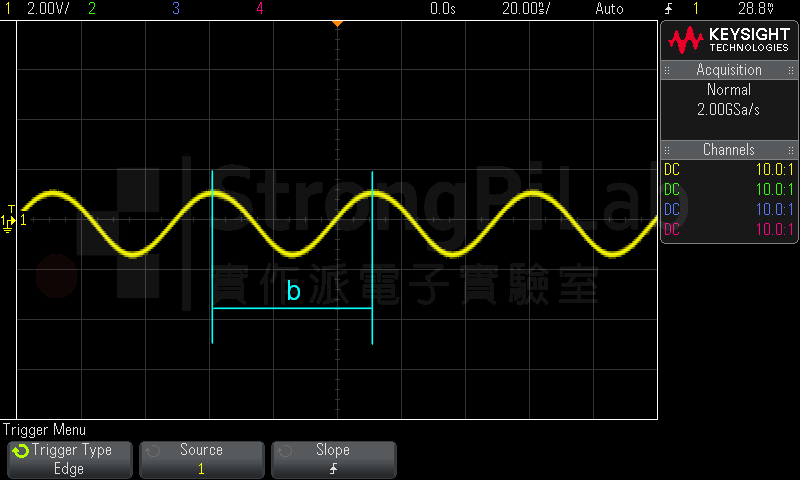
示波器弦波間的距離是週期（圖片來源：實作派提供）

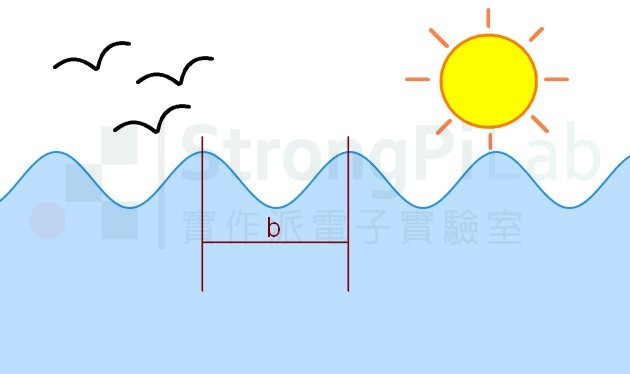
水面的波紋的距離是波長（圖片來源：實作派提供）

示波器的 b 稱為週期，水波紋的 b 稱為波長，不知道各位答對了沒有。如果你有堅強的物理背景，你應該會答對，如果你整天與示波器為伍，天天都在觀察波形，那麼在習慣的驅使下可能會有機會答錯，這兩個物理量畫出來的形狀實在太像，甚至概念也很像。

如果我們用繩子的震動來觀察，兩個波峰之間的間隔，可以用時間來敘述，也可以用距離來敘述。當你個別敘述的時候，用週期或是波長來稱呼這個間隔，看來沒有太大的問題，即便你混用，大家也不見得能發現差異。

但當討論波的行為時，我們會需要在同條繩子上仔細分辨這兩種物理量—週期與波長，因為要以數學來描述正在運動中的波，需要非常清楚明確的邏輯。

下面的弦波函數巧妙地將週期與時間合併在一起，當時間 t 固定時，它就是個在空間中凝結的波，當位置 x 固定時，它就是個隨時間擺盪的點，我想目前各位不會有什麼問題。

Asin (ωt−kx)
ω: 角頻率、t: 時間、k: 波數、x: 位置

我們都知道頻率是什麼，單位時間內波的震動次數，單位時間通常是 1 sec，若以正弦波的形式表示，震動一次角度需要走一圈，也就是 2π，所以角頻率 $\omega =2\pi f= 2\pi \frac{1}{T}$ ，其中 f 為頻率、T 為週期。

那上面的波數 k 是什麼？k 是單位長度內波的震動次數，單位長度通常是 1 m，若以正弦波的形式表示，震動一次角度需要走一圈，也就是 2π，所以波數 $k= 2\pi \frac{1}{T}$ ，其中 λ 為波長。

你有沒有發現，波數和頻率的思考邏輯完全一樣，差別只在：

既然波震動一次需要耗時週期 T，並且走了距離 λ，很自然的波傳遞的速度就是：

上面的例子只是一維的波動方程式，完整三維的波動方程式是個非常複雜又美麗的二次偏微分，空間與時間的觀念要非常清楚，否則很難在腦袋裡面建構它的樣子，還好現在軟體很發達，已經有模擬工具可以觀察到波的三維動態了，你看下面這樣的模擬動畫是不是很美。

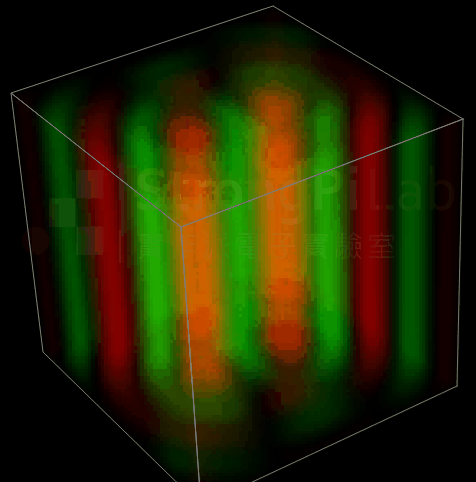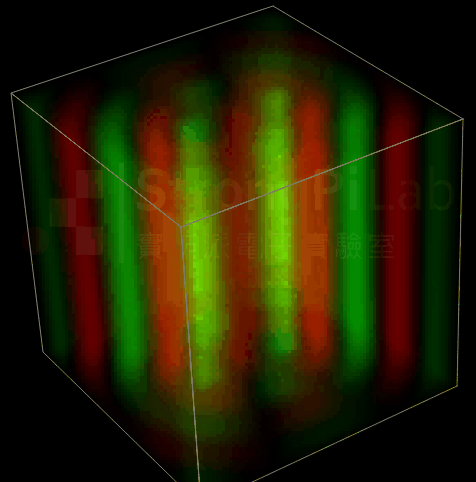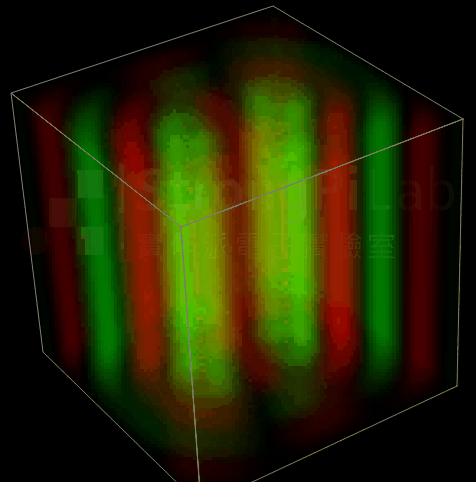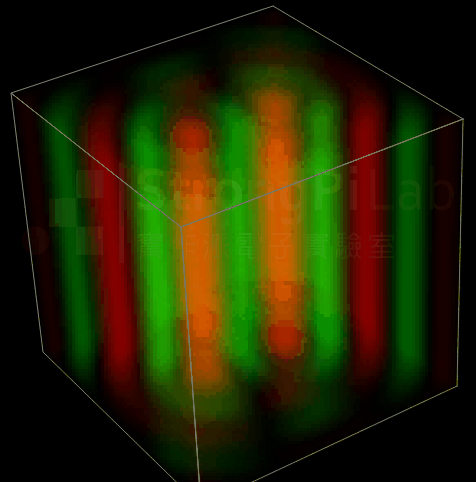
平行導線的波動狀態模擬（圖片來源：實作派提供）

（本文經同意轉載自實作派電子實驗室、原文連結；責任編輯：賴佩萱）

實作派電子實驗室（StrongPiLab）是一個著重知識與經驗的實作交流媒體，提供工程師們理論外的實務經驗，主要傳達電子產品與家電用品的正確操作概念與生活小常識、解說各種測試手法的技巧。