作者:文創造設計工作室/張宇文
1883 年,一位法國的數學家 Edouard Lucas 教授在雜誌上介紹了一個相當吸引人的題目「Tower of Hanoi」,中文翻為河內塔。
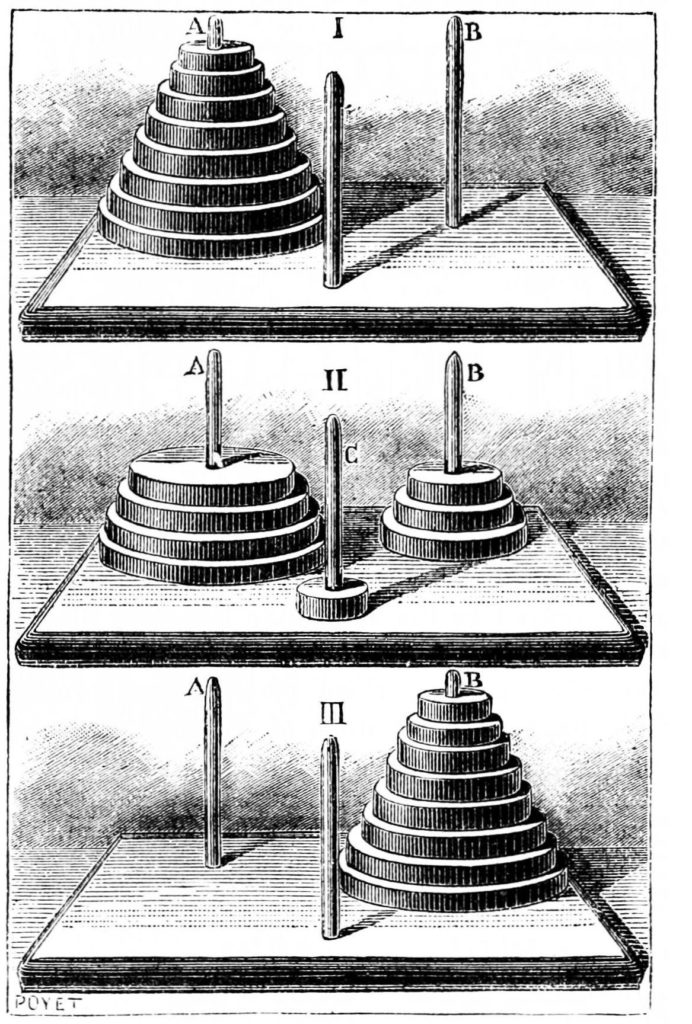
(圖片來源:KKnews)
這是一種結合實際操作與邏輯思考的遊戲,在「遊戲學」中屬於博弈類—個人挑戰棋弈,類似於華夏傳統的「孔明棋」。

(圖片來源:文創造提供)
這類型的個人思考型遊戲,也可以說是一種古老的「邊緣人遊戲」。傳說遊戲的故事背景是從印度的一座神廟開始,據說神廟位於宇宙的中心,在廟宇中放置了一塊上面插有三根長木釘的木板,在其中的一根木釘上,從上至下被放置了 64 片由小至大的圓環。
天神指示僧侶們:規定每次的移動中,只能搬移一片圓環,過程中必須保持圓環直徑較小的被放在上層。
如果有一天,僧侶們能將 64 片的圓環依規則全部移動至另一根木釘上,那麼世界末日即隨之來到,世間的一切終將被毀滅,萬物都將至極樂世界。
從此全世界有許多數學家開始研究,並從這個遊戲衍生出許多理論與研究,其中最有名的就是可以用最少的步數完成遊戲,或是增加不同遊戲規則來做一些變化。
本次文章,就是教大家如何利用簡單的繪圖設計製作出這組遊戲。
作品設計理念
本次設計的是最簡單的三層式的遊戲。

(圖片來源:文創造提供)
從傳統的遊戲說明圖中可以看到,遊戲分為一個底座、桿子(傳統的為三支)與不同直徑的圓盤。
平面設計
第一版繪製的主要目的是把架構畫出來,並確認組裝的可行性。

(圖片來源:文創造提供)
第二版時把厚度與比例的關係加到設計裡,並思考遊玩的舒適性,所以把底座從二層改成三層,也把圓環改為三層。
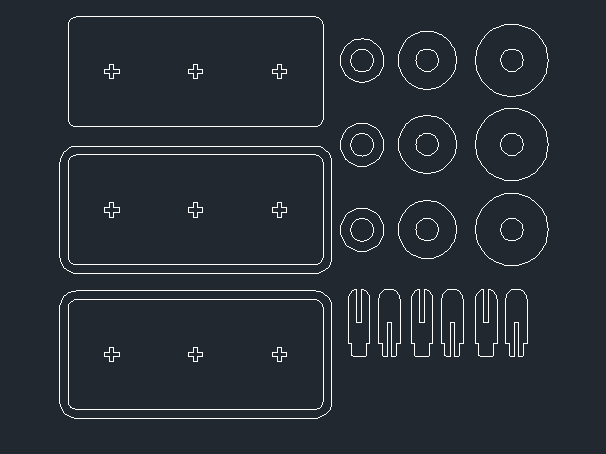
(圖片來源:文創造提供)
第三版主要是確認之後作品的組裝便利性,並思考如何讓失誤率降低。已往的圓環都是直接利用白膠黏合,考慮到現場可能沒有白膠,或是白膠黏歪之後放不進去竿子內,所以利用卡榫的方式做結合。

(圖片來源:文創造提供)
第四版也是所謂的上機版,可以說是假如要量產的送樣檔案。這時候就要來做「排版」與「微調」的動作,例如哪邊的空間可以利用,以節省用料,或是哪邊須要設計斷點,讓零件不會從木板上掉落,還有卡榫的部分是否需要預留尺寸讓組裝更便利。
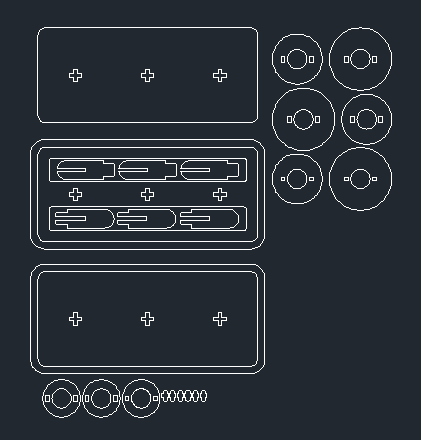
(圖片來源:文創造提供)
這部分用好後就可以進入打樣階段了。
立體圖
補充說明,一般文創造的做法是在第三版完成後就進行立體建模,一來除錯,二來可以看到整個成品的比例,不過這次的作品結構較為簡單,就直接上機打樣了。
打樣與組裝
打樣階段最重要的就是確認材質與功率,每個環節都會影響最後的品質。在組裝時也要注意是否有干涉或是焦邊太嚴重。
下面是打樣之後的組裝過程。
1. 底座:

(圖片來源:文創造提供)

(圖片來源:文創造提供)

(圖片來源:文創造提供)
2. 圓環:

(圖片來源:文創造提供)
基本解法
解法示範,只要記住兩個原則:
- 一次只能移動一個圓盤
-
小的圓盤一定要在大的圓盤上面

(圖片來源:文創造提供)
遊戲難度調整
目前常見的幾種擴增玩法如下:
- 增加圓盤數量
-
增加桿子數量,並規定每次必須放在不同的桿子上。
-
把圓盤變成雙色,並規定相同顏色不能從疊。
類似這些變異的玩法之外還有很多種,有興趣的朋友可以上網查看看。
遊戲中的數學小知識
在結合河內塔的時候,可能有些人會發現,他的解法為移動小環(簡稱 1 號),在移動中環(簡稱 2 號),在移動大環(簡稱 3 號),順序如 1213121 這種規律,如果放在傳統的中式童玩九連環,會發現是一樣的,是不是非常有趣呢?
有關河內塔的數學理論可以閱讀這篇文章>>>[離散數學]河內塔難題再下一塔
小結
童玩充滿著前人的智慧,而玩是人類的天性,可以說是小朋友最早的學習管道。透過自己設計玩具,並從中學習其中的邏輯與智慧,最終創造出新的遊戲,不僅符合創客精神,同時也蘊含各種面向的學習;在整個過程中,最重要的是,設計者是真的為了想要學習而引發後續的動作,這就是玩樂教育最大的特色,因為「想玩」所以學習。
如果在學習中發現其他更好玩有趣的事,這個過程就會一直的延伸,最後「主動學習」就會變成一種習慣,而在不停的測試與探索中,累積失敗經驗後,再創新,也正是文創造最重視的實戰的精神。
(責任編輯:賴佩萱)
- GIF動畫從頭說起-細說翻頁書的歷史(下) - 2024/03/29
- GIF動畫從頭說起-細說翻頁書的歷史(上) - 2024/02/26
- 科學玩具-彈珠小海龜 - 2024/01/31
訂閱MakerPRO知識充電報
與40000位開發者一同掌握科技創新的技術資訊!



