作者:Bird
上篇文章我們從壓電效應開始,介紹了石英晶體如何運用壓電效應成為頻率穩定的元件以及石英晶體的切割。這一次我們要來談談石英晶體在電路裡的角色。
震盪電路 #
石英晶體既然是時脈元件,當然就要搭配振盪電路來產生時脈訊號。我們先來看一個最簡單的振盪器。拿一個 not 邏輯閘,把它的輸入和輸出接在一起,構成這樣的電路:
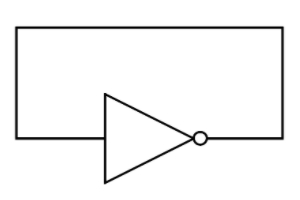
(圖片來源:Bird 提供)
Not 邏輯閘的真值表很簡單:
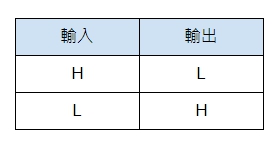
(圖片來源:Bird 提供)
如果我們把 not 邏輯閘的輸入和輸出接在一起,乍看之下好像會形成一個不合理的邏輯悖論,因爲這不是量子電腦,邏輯閘的兩端不能既相同(因爲被接在一起)又不相同(因爲真值表是這麼說的);但在真實世界中,這樣的電路是存在且可以運作的,因爲這牽涉到一件真值表中沒有說的事:傳遞延遲 (propagation delay)。
傳遞延遲是真實世界中所有的邏輯閘都會有的一個特性,它的定義就是當邏輯閘偵測到輸入的狀態改變後,到輸出真正改變的時間差。
以上面這個電路來說,假設在現在這個 moment,not 閘的輸入是 low,那麼經過一小段時間的 propagation delay 後,它的輸出會變成 high。當輸出變成 high 後,馬上經由我們接的這根線又傳回了輸入,這時邏輯閘偵測到輸入變成 high 後,又要經過一小段時間,輸出才會變成 low,如此周而復始,這個電路就會不斷在 high 和 low 之間交替,或者說震盪。它的訊號波形會是這樣的:
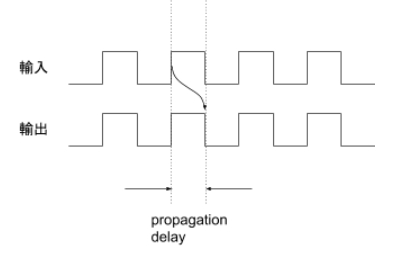
(圖片來源:Bird 提供)
圖中那個彎彎的箭頭代表波形圖中的因果關係,也就是「因爲發生這件事,所以才發生那件事」。以上圖來說,因爲輸入變成 high 了,經過了一小段時間的 propagation delay 之後,輸出就會變成 low。
這個電路是將 not 閘頭尾接在一起變成一個環路,所以這樣的振盪器叫做「環形振盪器」(ring oscillator),可以算是所有震盪器的邏輯概念基礎,它跟「貓會追著自己的尾巴跑」這件事也有某種程度的相似性。
難以駕馭的 Delay #
聰明的讀者一定可以從波形圖中發現,原來這個振盪器的震盪週期就是 not 邏輯閘的 propagation delay 乘以二,換句話說,它的震盪頻率就是:
FOSC = 1 / (2*TPD) where TPD is the propagation delay of the not gate
我們來看一個實際的例子。以 74LVC04A 這顆 not 邏輯閘的始祖爲例,我們來查查看它的 propagation delay 是多少:
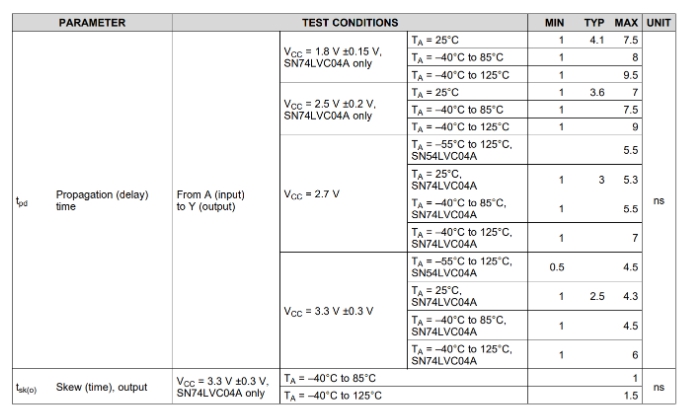
(圖片來源:Bird 提供)
沒想到 datasheet 中列出的 propagation delay 居然有這麼多數字,而且範圍還不小。
沒錯,CMOS 邏輯閘的 propagation delay 受到 IC 內部電晶體的開關特性影響,會隨著溫度、電壓而改變。原則上供電電壓越高,MOSFET 的切換速度會越快,因此 propagation delay 會越短。以工作在 25 ℃ 的情況來看,VCC =1.8 V 時典型的 propagation delay 是 4.1 ns,因此如果我們用它來做上面那個電路,它的震盪頻率就會是:
FOSC = 1 / (2*TPD) = 1 / ( 2 * 4.1 * 10E-9) = 121 MHz
但如果供電電壓增加到 3.3 V,TPD 會減少到 2.5 ns,這時震盪頻率就會變成:
FOSC = 1 / (2*TPD) = 1 / ( 2 * 2.4 * 10E-9) = 200 MHz
看起來好像可以用這樣的電路做一個可以用電壓控制頻率的震盪電路。雖然理論上這樣是可行的,但卻有個很現實的問題:它很不準。
我們剛剛用來計算震盪頻率的 propagation delay 都是典型值,但在 datasheet 中列出來的可能範圍其實蠻大的。以 1.8 V 供電時來說,它的 propagation delay 可能從 1 ns 到 7.5 ns,如果換算成頻率,它振出來的頻率就可能從 500 MHz 到 133 MHz 都有,而且你不能說它有問題,因爲這個 propagation delay 都在 IC 的規格範圍內。
因此單單用 propagation delay 來控制 ring oscillator 的震盪頻率,並不是一個好方法。
這時就輪到石英晶體上場了。
進擊的石英晶體 #
我們在上一回提過石英晶體的等效電路長這樣:
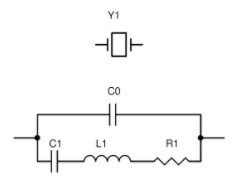
(圖片來源:Bird 提供)
而且它有一個看起來很恐怖的等效阻抗數學模型:
Z(s) = ( 1/(sC1) + sL1 + R1) // (1/sC0)
我們把上面那個等效電路經過很複雜的推導之後,會得到一個這樣的圖,橫軸是頻率,縱軸是阻抗:
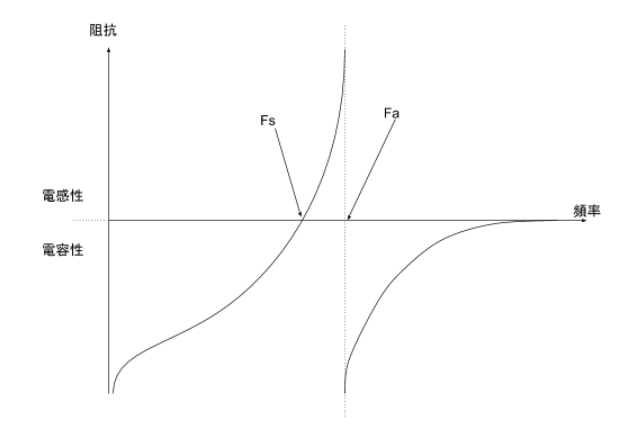
(圖片來源:Bird 提供)
石英晶體的阻抗會隨著加在它上面的訊號頻率不同而變化,這是這個元件的奇妙之處。
當頻率很低的時候,石英晶體對電路來說看起來會像個電容器。這很合理,我們上次聊過石英晶體內部的結構,它是在切割過的石英晶體上貼上兩個電極,而由於石英是絕緣材料,貼上兩個電極後,它就成爲一個電容器。
但當我們對石英晶體加上訊號之後,它就不是純的電容器了。由於壓電效應的關係,石英晶體會跟著訊號變形、震動,而且在每次「回彈」的時候還會因爲逆壓電效應而吐一些能量回來,這也是爲什麼石英晶體的等效電路中有電感的原因。
當訊號的頻率越來越高,石英晶體等效電路中電感的特性會越來越強,抵消掉它電容器的特性,到了某個頻率以上,石英晶體在電路中看起來就像個電感了。這個從電容性變爲電感性的頻率,稱之爲這個石英晶體的「串聯諧振頻率」(series resonant frequency),或是 Fs。
如果頻率再繼續往上增加,石英晶體的等效感抗會持續增加,而且到了某個頻率時感抗會急劇增加,並在一個不連續的點上突然變回容抗。這個讓石英晶體特性不連續,或是說難以捉摸的頻率,稱之爲這個石英晶體的「反諧振頻率」(nti-resonent frequency),或是 Fa。
在 Fs 和 Fa 中間的這段頻率,石英晶體會呈現穩定的電感性;一般來說,石英晶體的這兩個頻率差距很小,而石英晶體所表示的工作頻率,就在這兩個頻率中間。如果我們把石英晶體放到前面講的 ring oscillator 電路中:

(圖片來源:Bird 提供)
而當石英晶體變成電感性的時候,這個電路就變成:
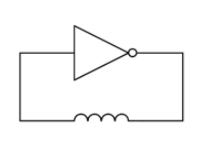
(圖片來源:Bird 提供)
這個電路看起來有點眼熟,但又好像少了點什麼。我們幫它加上兩個電容器好了:
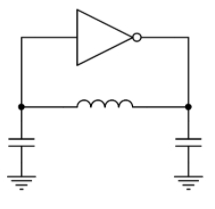
(圖片來源:Bird 提供)
咦!這不就是考畢子振盪器(Colpitts oscillator)的電路嗎?沒錯,這個電路就是一個典型的、利用電感和電容控制振盪頻率的考畢子振盪器。
考畢子振盪器中的 L-C-L 電路構成一個低通濾波器,連接 inverter 的輸出和輸入。因爲低通濾波器會限制能通過它的最高頻率,因此只有某個頻率以下的訊號能夠從 inverter 的輸出被送回輸入,你可以說它「限制」了這個振盪電路的頻率。
我們前面在討論用 not gate 或 inverter 直接構成 ring oscillator 時,是讓 inverter 在完全不受限制的狀況下,只靠它自己的 propagation delay 來工作。事實上這個靠著 propagation delay 而振出來的頻率,是這個振盪電路所能工作的最大頻率,它可以在這個頻率以下的任何頻率工作。
我們可以藉由介入從輸出連接回輸入的這條回授路徑,來控制振盪器的頻率,只要它不超過那個最大工作頻率就好,這就是考畢子振盪電路工作的原理。
再把上面那個電感的符號換回石英晶體:
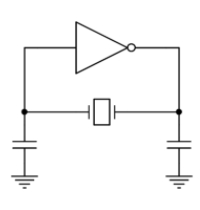
(圖片來源:Bird 提供)
這就是典型的石英晶體振盪電路,有沒有覺得它似曾相識?幾乎所有可以用石英晶體當作 clock 訊號來源的 IC,都是用這樣的電路連接石英晶體,只是那個 inverter 做在 IC 內部,我們看不到,但外面的石英晶體和兩個小電容器這樣的接法,相信大家一定不陌生。
由於石英晶體只有在 Fs 和 Fa 之間的頻率區間呈現電感性,也才能讓這個考畢子振盪電路振起來,因此這個電路就只會在這個頻率振盪。我們放 12 MHz 的石英晶體,它就振 12 MHz,不會有其它的頻率;我們放 24 MHz 的石英晶體,它就振 24 MHz,不會有其它的頻率。
小結 #
這次我們介紹了利用 inverter 構成的、最基本的振盪電路 ring oscillator,並且嘗試用了一個很直觀、不靠數學模型推導的方法,來介紹石英晶體在振盪電路中的角色;下一回我們會繼續探討這個電路中的兩個小電容器對電路有什麼影響,以及該如何決定它們的數值。
(責任編輯:賴佩萱)


