作者:Ted Lee
遞迴是程式自己呼叫自己的一種抽絲剝繭的解題計巧。
因為這類的大問題是由其相同型式(pattern)的小問題所疊代(iterate)而增長而成的。所以,當問題空間(problem space)降低至易於處理的小大(size)時,我們就很容易從小問題的答案再往上一層一層回溯(backtrack)而組合出原大問題的解答。
例如:欲求數列(sequence) 1, 1, 2, 3, 5, … 的第 10 項為何數字,我們可以發現,這串數列好像有一個隱含的規律(implicit regularity)是:第 i 項是前兩項 (i-2), (i-1) 的和,當 i > 2 時。例如:5 = 3 + 2。
在表 1 的「10 大項目之 10」的 4 個實例(可從此處下載)中將探討電腦科學(Computer Science,CS)中這類的經典(classical)遞迴問題──將大問題拆解(divide)為小問題,再將小問題的答案逐步組合(combine)為大問題的解答。
前題:大問題和小問題具有相同的結構性(structure)!
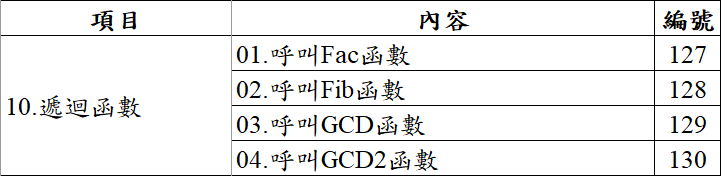
表 1:10 大項目之 10
遞迴分析
在本小節中,我們甞試使用運算思維(computational thinking)的法則來分析費式數列問題:
步驟 1:拆解(decomposition)。我們設計了表 2 的費氏數列空白觀察表(observation table)來推敲此數列的生成(generate)過程。其結果如表 3 所示。

表 2:空白觀察表

表 3:費氏數列前十項觀察表
步驟 2:模式辨別(pattern recognition)。從表 3 中,我們似乎可以看出 5 = 2 + 3,即第 n 項的值為前兩項之和。
步驟 3:抽像化(abstraction)。根據以上的觀察,我們大膽的以圖 1 這個遞迴公式(recurrence formula)來猜測費氏數列的表現。註:讀者們可援用數學歸納法(athematical inducation)來證明它的正確性。
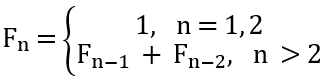
圖 1:費費數列的遞迴公式
步驟 4:演算法(algorithm)。根據圖 1 的公式,我們可以圖 2 的流程圖來表式費氏數列的演算方法。
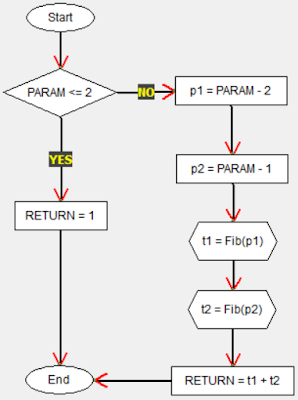
圖 2:費式數列的流程圖
原始問題
本文只詳述「10-02.呼叫Fib函數」:請計算費氏數列(Fibnacci number)第六項的值,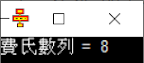 。其他三例請讀者們自行練習。
。其他三例請讀者們自行練習。
流程圖與 Python 語法對轉
首先,函數(function)的語法請參考前著「以 fChart 馭 Python:函數」一文。緊接著,從圖 中我們可以看到 Fib(n) = t1 + t2 = Fib(n – 1) + Fib(n – 2),n = 6。
其中,
Fib(6)
= Fib(5) + Fib(4)
= [Fib(4) + Fib(3)] + Fib(4) = 2 * Fib(4) + Fib(3)
= 2 * [Fib(3) + Fib(2)] + Fib(2) + Fib(1) = 2 * Fib(3) + 3* Fib(2) + 1 = 2 * Fib(3) + 3 * 1 + 1 = 2 * Fib(3) + 4
= 2 * [Fib(2) + Fib(1)] + 4 = 2 * [1 + 1] + 4 = 8
遞迴程式的撰寫格式為:
def Fib(n):
if (n <= 2):
return (Fib(n - 1) + Fib(n - 2)
else:
return 1
數後,根據流程圖將 Python 程式轉換妥後以「10-02.呼叫Fib函數.py」存檔執行後就能看到如圖 3 所對應的執行結果。
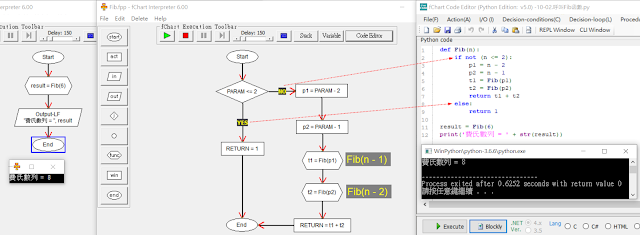
圖 3:根據流程圖手動轉換為 Python 語法以求得 Fib(6) 之值
(作者為本刊專欄作家,本文同步表於作者部落格,原文連結;責任編輯:謝涵如)
- 用GenAI自動拆解程式碼學習:GenAI時代的新程式學習法 - 2025/12/29
- 「動手」之前 你需要了解電腦系統的基礎知識點! - 2025/11/28
- GenAI拆解學習:以「健康手環監測系統」示例 - 2025/10/23
訂閱MakerPRO知識充電報
與40000位開發者一同掌握科技創新的技術資訊!


