【自學AI#3】你的K個好鄰居，深度學習認識kNN

Posted By 賴建宏 on 5 月 20, 2019 in Edge AI開發地圖, 教學文 | 0 comments

作者：賴桑

在第二集中，我們看了 ANN ，才發現原來就是個計算機，沒關係，還沒到死心的地步，不是還好幾種？我們這次再看另外一個經典： kNN 。

什麼是 kNN ？

在開始下手之前，我們先來看一下 kNN 的前世今生， kNN 的全名叫做 K Nearest Neighbor ，顧名思義就是 k 個最接近你的「鄰居」，那這所謂的鄰居…是怎麼來的呢？先看一下圖：

kNN解釋圖（圖片來源：賴桑提供）

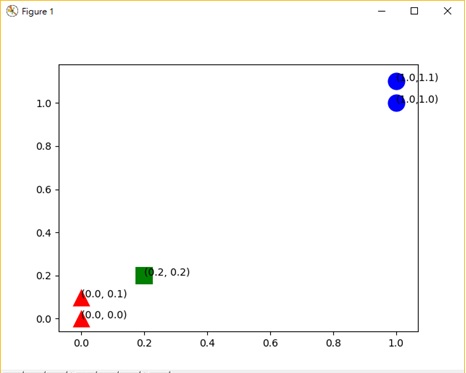
綠色的方塊，是我們的新資料；目前電腦裡面可以看到有藍色圈圈、紅色三角形兩種，那我們就把藍色圈圈稱為 A 組，紅色三角形稱為 B 組吧， kNN 的做法，就是根據我們人類指定的 k 這個數值，算出來綠色方塊為圓心下，到底是藍色圈圈代表 A 組靠近新資料數量多，還是紅色三角形代表 B 組靠近新資料數量多？如果算出來 A 組比較多，那就加入 A 組，反之，如果是 B 組比較多，那就加入 B 組。

先別想到電腦上，想像你住的社區有人贊成行人穿越區應該拓寬避免人車爭道，另外也有人說應該先維修社區老舊的緊急發電系統，問題是…管理委員會的預算只夠花在這些工程議題的其中一項上。於是乎，你就會開始「評估」，到底應該要站哪一邊。這就 kNN 的基本精神─分類應用。

kNN 所謂的「鄰居」也能對照到實際上社區裡的鄰居，對電腦裡面，那就是剛剛分的藍色圈圈與紅色三角形，這些都是你的鄰居。所以根據上圖，你的鄰居有…四個，可是目前分成 A 與 B 組，就像各自支持社區中不同的公共建設議題，同樣的意思。

kNN 計算

看過了 kNN 介紹，會覺得其實 kNN 並沒有很複雜的學習，說白了就是記憶而已，因此在術語上，我們通稱像 kNN 這種只是單純把結果「背」的 AI ，歸類成 lazy learning 。可是…其實不是那麼簡單，你沒注意到有一個關鍵沒提到嗎？就是「評估」，電腦怎麼可能懂得什麼評估，人告訴電腦怎樣去計算，把計算的結果拿來判斷，這才是評估。

所以啦！所謂的評估，電腦只用算式來算，自己在設定的 k 之下的範圍中，這裡面哪些最多，然後就跟台語講的「西瓜偎大邊」一般地歸為那一組。

問題這怎麼算呢？分成三步驟：

決定 k 值
求每個鄰居（已有資料）跟自己（新資料）之間的距離
找跟自己最近的 k 個鄰居，看裡面哪一組數量較多，就加入哪一組
如果還是沒辦法決定在哪一組，回到調整 k 值，再繼續

這裡提供一個範例程式，給大家試試看；當然執行這個範例程式前，得先裝好 Numpy、Scipy、Matplotlib 這幾個 Python 的套件：

# -*- coding: utf-8 -*-

import sys  
import os 
import time
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
import operator


reload(sys)
sys.setdefaultencoding('utf-8')

def createDataSet():
    group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels

# cos夾角求距離
def cosdist(vector1,vector2):
	Lv1 = sqrt(vector1*vector1.T)
	Lv2 = sqrt(vector2*vector2.T)
	return vector1*vector2.T/(Lv1*Lv2)
    

# kNN
# 測試用資料：testdata
# 訓練集：dataSet
# 所有分類的標籤：labels
# k:k個鄰居
def classify(testdata, dataSet, labels, k):
	# 訓練集有多少資料
    dataSetSize = dataSet.shape[0]    
    # 算testdata和dataSet間的距離
    #
    diffMat = tile(testdata, (dataSetSize,1)) - dataSet
    #
    sqDiffMat = diffMat**2
    #
    sqDistances = sqDiffMat.sum(axis=1)
    #
    distances = sqDistances**0.5
    print distances
    # 根據距離排序，排序結果就是index
    sortedDistIndicies = distances.argsort()        
    classCount={}     
    # 取得k當參考         
    for i in range(k):  # i = 0~(k-1)  	  
    	# 根據前面排序得知對應的類別
        voteIlabel = labels[sortedDistIndicies[i]]
        #
        # 
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    # 丟回最高一項
    return sortedClassCount[0][0]

k=3
testdata=[0.2,0.2]
dataSet,labels = createDataSet()


fig = plt.figure()
ax = fig.add_subplot(111)
indx = 0 
for point in dataSet:
	if labels[indx] == 'A' :
		ax.scatter(point[0],point[1],c='blue',marker='o',linewidths=0, s=300)
		plt.annotate("("+str(point[0])+","+str(point[1])+")",xy = (point[0],point[1]))
	else:
		ax.scatter(point[0],point[1],c='red',marker='^',linewidths=0, s=300)
		plt.annotate("("+str(point[0])+", "+str(point[1])+")",xy = (point[0],point[1]))	
	indx += 1

ax.scatter(testdata[0],testdata[1],c='green',marker='s',linewidths=0, s=300)
plt.annotate("("+str(testdata[0])+", "+str(testdata[1])+")",xy = (testdata[0],testdata[1]))		

plt.show()
print classify(testdata, dataSet, labels, k)

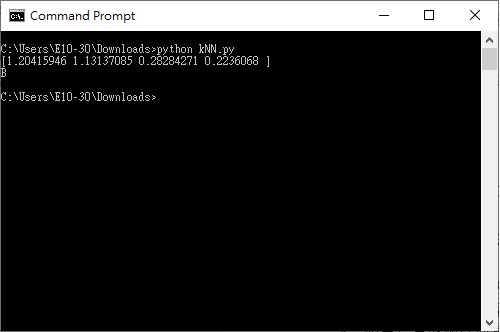
接著用你的命令提示字元，透過 python kNN.py 來執行；執行後應該會看見最上面的那張圖，有綠色的方框、藍色圈圈與紅色三角形，當關掉繪圖的視窗後，你應該可以看到計算出來的結果，應該分成 B 組：

範例程式的計算結果（圖片來源：賴桑提供）

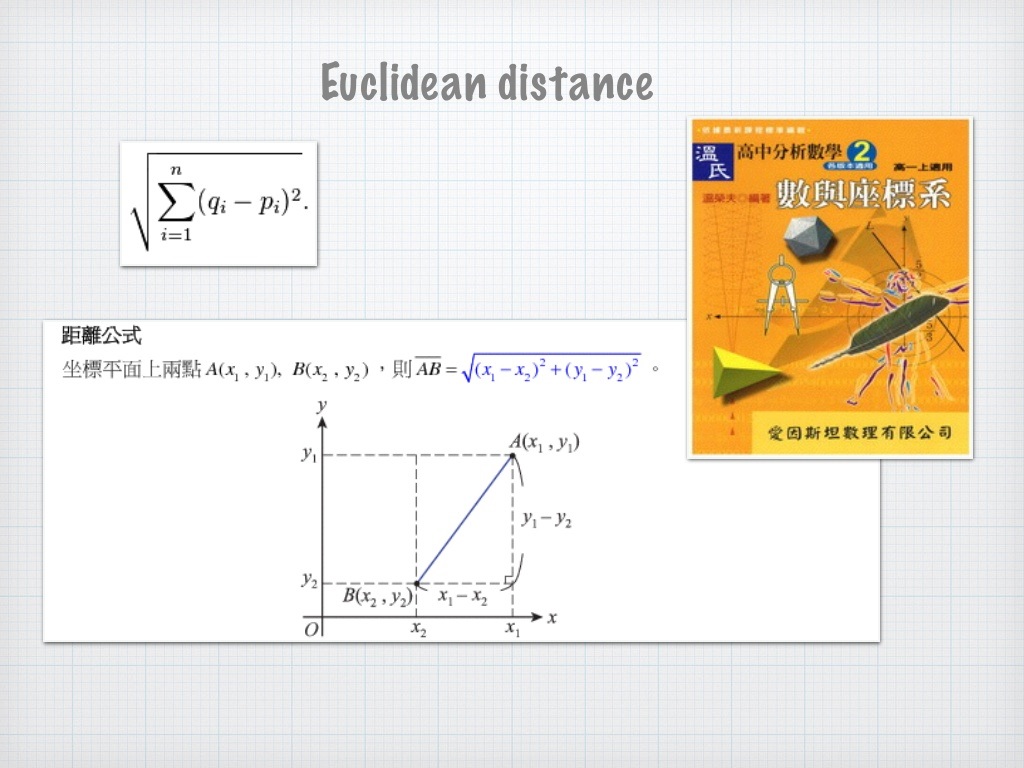
可是…這一個個鄰居的距離怎麼算呢？用高中數學就可以啦！看一下這個圖回想一下：

大家還記得高中學過的數與座標嗎（圖片來源：賴桑提供）

因此…把圖中的 X 和 Y 帶入我們的，就算出來啦，不過，可不只這種計算距離的方式，因為對 kNN 來說，所謂距離其實指的只不過是，「差異有多大」的估算而已，比如 kNN.py 這個範例程式，我其實是用 cos 夾角的做法：
$cos\theta = \frac{A}{\left | A \right |\left | B \right |}$

這集超考驗高中數學（圖片來源：賴桑提供）

除此之外，像是：明可夫斯基距離、曼哈頓距離、柴比雪夫距離、夾角餘弦、漢明距離、傑卡德相似係數…一大籮筐都有人用，記住，那只是在評估「差異有多大」，中心思想不能錯。

向量化

至於 X 和 Y 代表甚麼？我們常聽到一堆書上講如何甚麼「向量化」，事實上 X 和 Y 就是兩個向量，而「向量化」這三個字真正說的，就是找到代表的意義！好比 X 代表年齡、 Y 表示身高…等，把這些度量衡的意義找到，通過數據的方式呈現。

那 X 和 Y 怎麼會在一起還垂直？其實並沒有沒規定橫軸、縱軸，畫成線條只是為了容易看懂， X 、 Y 如果有交會（圖上那個垂直交點），那表示這兩者之間有甚麼關係，所以根據兩者的數據變化觀察而已。

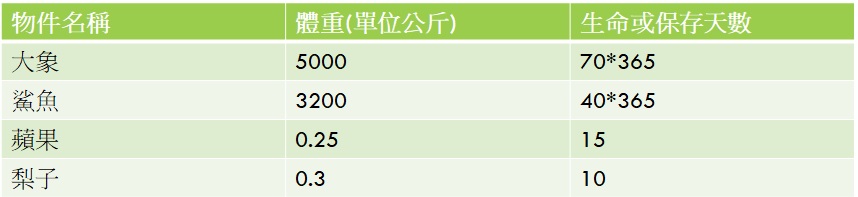
那電腦又是怎麼處理的呢，很簡單，就是做成表。

套用老師上課的講法：「所謂向量就是一個數值，然後具有方向的代表」…向量就是「方向」和一個「數值」，其實從圖還有前面的描述就看懂了吧？方向其實就是個代表性的意義，也就是圖裡面的直欄：體重、生命或保存天數。

這樣的話， kNN 也可以如法泡製了，目前的資料都一筆一筆存入關聯是資料庫 Relational Dtatabase ，不同的欄位就是不同的向量；當然，要套算式去求最近的距離，所以說…那些欄位最好是：數值。

最後，到底 kNN …是真的要在加入新資料的時候，把每一個已有資料都再算一次距離嗎？動動腦筋，既然有資料庫系統可以幫忙，那我每次都先根據 k 去按照欄位先排序，從排序後的結果撈k個出來，這樣不是就只要算 k 個就好，比如用 SQL 指令：

SELECT ID, … FROM TABLE ORDER BY FIELD1, FIELD2…

這樣只要抓最前面的 k 筆來算距離，是不是就成功了，那沒有資料庫，把資料放到陣列然後先排序，只抓前面的 k 個，不是一樣嗎？好比說用快速排序法 Quick Sort ，排序過後由小到大取最前面的 k 個來做 kNN ，搞定。

小結

kNN 這個老一代的分類演算法，只要稍微動動腦筋，還是很好用，不過，這種方法比較擔心，就是可能發生類似八掌溪「人球」事件，因為新資料一加入，就根據算式開始計算距離，而這時候很可能發生 ─ 剛好勢均力敵的現象（行話叫做：對於局部資料結構非常敏感），這也是 k 常常為奇數的原因！因為如果是奇數，那總是會比來比去有一邊多一個的機會比較大，再不然…還是得要靠人力排除啦！

（責任編輯：楊子嫻）