Posted By Liang Bird on 4 月 15, 2019 in 教學文, 綜論 | 6 comments

作者：Bird

在很多 maker project 中，常常會有偵測溫度需求，很多人的第一個 Arduino 專案也往往跟環境溫度測量有關。這次我們就來聊聊常見的溫度感測方式，以及它們的原理。

溫度係數

19世紀以前，其實人們就已發現有些材料的電阻會隨著溫度變化而有所不同。1833 年法拉第在研究硫化銀的特性時，發現硫化銀的電阻會隨著溫度的上升而下降。他將硫化銀製成的零件串聯在一個電路上時，發現當硫化銀被加熱時，流過電路的功率會顯著增加。

這種「隨著溫度上升電阻變小」的特性，我們稱之爲「負溫度係數」電阻，而有著這樣特性的電阻零件就稱之爲「負溫度係數熱敏電阻」。講到這，我們得先來定義一下「溫度係數」這件事。我們知道很多電子零件都有各自的特性，像是電阻、電容、電感、頻率等，而這些特性隨著溫度變化的「比例」，就稱之爲「溫度係數 k」。

（R2-R1）/R1 = k（T2-T1）

等號的左側是一個無因次的比例值，通常會表示為百分比或是 ppm，因此溫度係數的單位通常都表示爲「%/℃」或「ppm/℃」。它的意思就是「溫度每變化 1 ℃，零件的數值變化百分之多少」。

舉例來説，一個電阻在 25 ℃ 時的阻值是 10 KΩ，到了 45℃ 時變成 9 KΩ，那麽它在這段溫度變化區間的溫度係數就是：每 ℃ 負百分之零點五。

（9K – 10K）/10K/（45℃ – 25℃）= -10%/20℃ = -0.5%/℃

如果電阻的阻值變化隨溫度上升而遞增，算出來的溫度係數就會是正的，反之則是負的。對，溫度係數可以是正的也可以是負的，端看電阻的變化量與溫度的變化是同方向還是反方向。

事實上現在我們已經知道，大部分的半導體材料，由於溫度上升時載子（自由電子或電洞）的密度會提高，導電度都會增加，因此大部分的半導體材料都是負溫度係數的，而有一些陶瓷材料或是高分子聚合物材料，則有正溫度係數電阻的特性。

熱敏電阻

在一般的電路應用中，負溫度係數熱敏電阻和正溫度係數熱敏電阻都用得到，不過它們的應用場合不太一樣。

正溫度係數熱敏電阻稱之爲 PTC termistor，常常被簡稱為 PTC，其實就是「Positive Temperature Coefficient」的縮寫，這種零件的電阻會隨著溫度的上升而增加，但不是那麽線性（通常在某個溫度以下變化不大，過了某個溫度之後會開始快速攀升），如下圖所示：

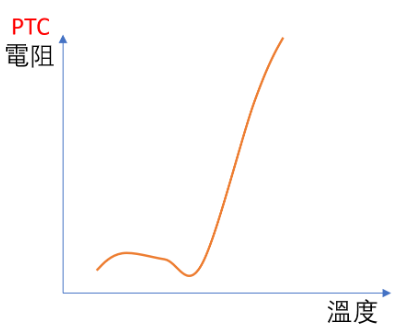
PTC 電阻在某個溫度以下變化不大，過了某個溫度之後會開始快速攀升（圖片來源：Bird 提供）

這種電阻隨著溫度快速上升的特性，讓 PTC 很適合用來做保護元件。當流過 PTC 的電流過大時，因爲 PTC 本身的電阻也會有功耗，這個功耗就會使 PTC 發熱，一旦 PTC 因爲自身的發熱讓它的溫度超過臨界值，它的電阻就會開始快速上升，進而抑制流過的電流，讓流過 PTC 的電流回復到正常值。

因爲這樣的特性，PTC 熱敏電阻常常被拿來做「自復式保險絲」。一般的保險絲電流過大它就熔毀燒斷，得換個新的才能修復，而自復式保險絲顧名思義就是，它在電流過大時會將電路斷開（或是用一個很大的電阻「幾乎」將電路斷開），但在過大的電流消失之後一小段時間之後，因爲溫度回到正常的範圍，它的導電性就會恢復。

一般我們常常在 USB 集線器中看到的圓盤狀零件，就是 PTC 熱敏電阻做成的自復式保險絲：

USB 集線器中由 PTC 熱敏電阻做成的自復式保險絲（圖片來源：Bird 提供）

這種自復式保險絲多半用高分子聚合物的正溫度係數電阻材料做成，因此常常被叫做 poly switch，poly 就是 polymer（聚合物）的意思。

不過正溫度係數熱敏電阻並不適合拿來量測溫度，主要是因爲它的電阻隨溫度變化的特性並不是那麽線性，甚至溫度係數在不同的溫度區間變化很大。

而負溫度係數熱敏電阻（NTC thermistor）的特性就比正溫度係數熱敏電阻要好上很多。NTC termistor 的電阻對溫度曲線通常長這個樣子：

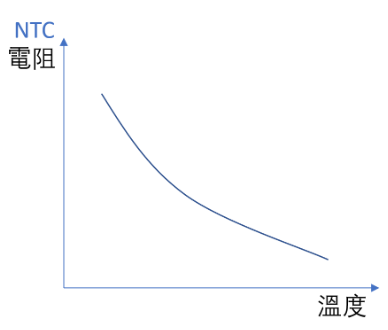
負溫度係數熱敏電阻隨溫度上升而下降（圖片來源：Bird 提供）

NTC 的電阻對溫度變化曲線雖然不是百分之百線性，但在一定的區間内（通常是數十 ℃）可以假設它是線性而不會有太多的誤差。

實務上，由於 NTC 的電阻對溫度變化曲線不是線性的，我們會用一個對數曲線來逼近它。在大部分的 NTC 熱敏電阻產品中，會有一個叫做 B 的特性常數，跟這個對數曲線有很重要的關係。

我們來看個實際的例子。

在 Murata 的 NTC 熱敏電阻產品中，每個產品都會列出這麽多特性：

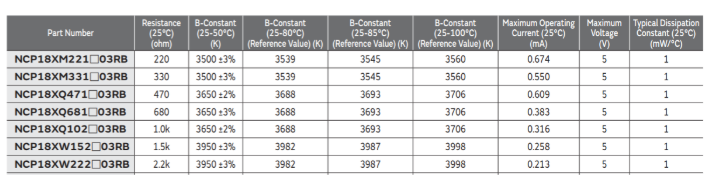
（圖片來源：Bird 提供）

而關於這個「B-Constant」，在 datasheet 中有這麽一個計算式：

R_T = R₀ * e ^{B（1/T – 1/T0）}

遇到這種看起來很可怕的數學式子，征服它最簡單的方法就是實際算算看。於是我們拉一個試算表來算算看 NCP18XM332 這顆 NTC 熱敏電阻在不同溫度下 RT 的變化。這顆 NTC 熱敏電阻在 25 ℃ 時的電阻是 220 Ω，而既然它是負溫度係數，它的電阻應該會隨著溫度上升而降低。至於是不是這樣，我們來算算看就知道了。

但是上面的表中有好幾個 B-Constant，到底該用哪一個呢？事實上每個 B-Constant 都有交待它適用的溫度範圍，我們就先來算算 25-50 ℃ 這一個吧。

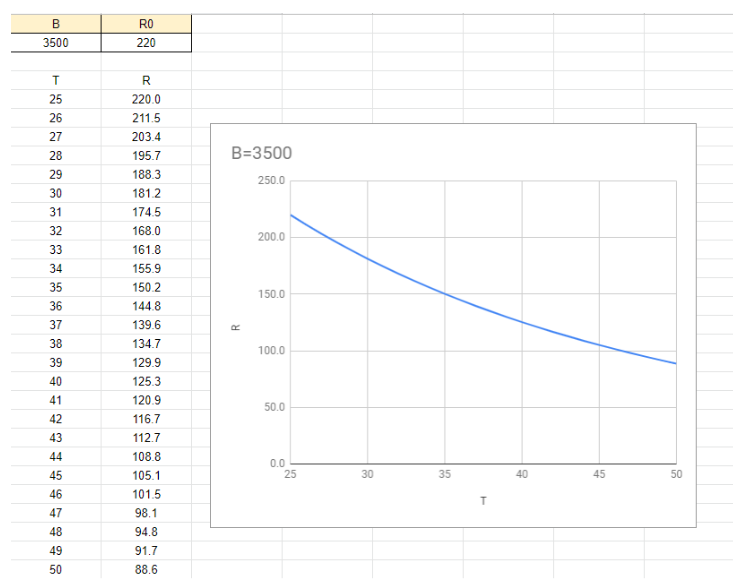
隨著溫度上升，電阻迅速下降，到 50℃ 時已經只剩下 88.6 Ω 了（圖片來源：Bird 提供）

我們再來算一下 25-80 ℃ 的特性，用規格書中第二個 B-Constant 3539。

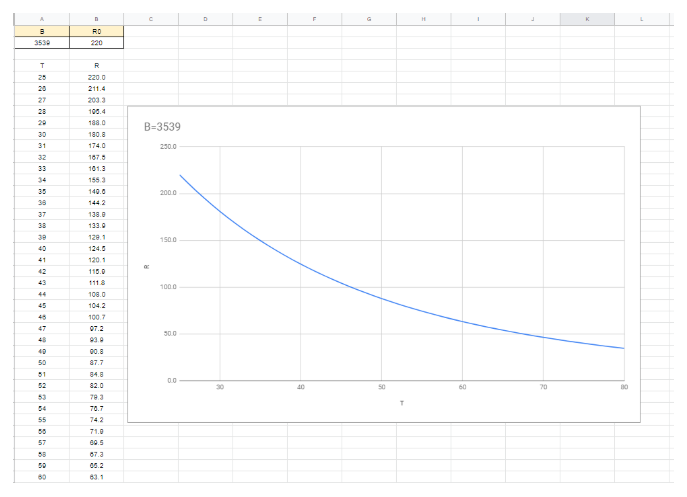
溫度範圍較大時，電阻的變化就沒有那麽線性，這個曲線彎得更明顯（圖片來源：Bird 提供）

我們如果把兩個 B-Constant 畫出來的曲線曡在一起：

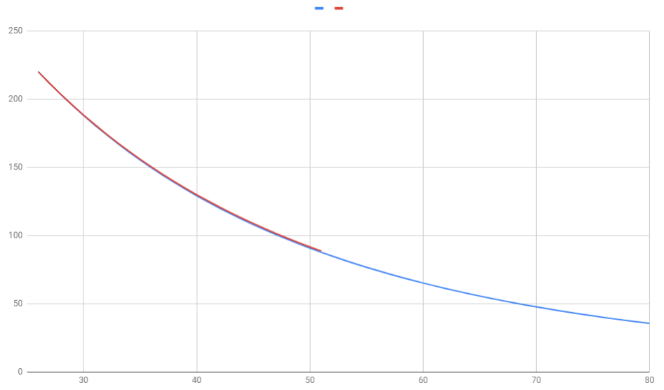
（圖片來源：Bird 提供）

可以看出來它們略有差距，但差距不大。但如果用 25-50℃ 的 B-Constant 畫到 80 ℃，差距就會比圖中顯示的還大一些。

因此，決定用哪個 B-Constant，就取決於你打算用這個 NTC 熱敏電阻測量溫度的區間。原則上，區間越小精度越高。

與 MCU 的連接

實務上要用 MCU 來讀取 NTC 熱敏電阻的輸出，可以用分壓電路。以上面那顆 NCP18XM221 爲例，如果我們要用一個 ADC 輸入範圍是 0 – 3.3V 的 MCU 來測量它的輸出，我們可以用以下這個電路：

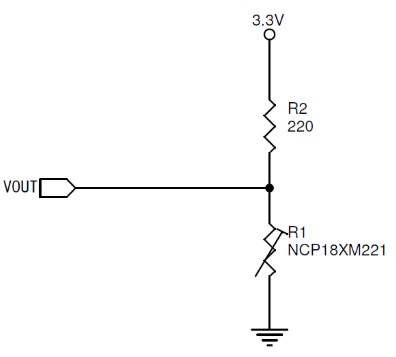
（圖片來源：Bird 提供）

前面算過了，NCP8XM221 在 25℃ 時的電阻是 220 Ω，此時 V_OUT 上的分壓是：

V_OUT = 3.3*（220/（220 + 220））= 1.65 V

而當溫度上升到 80℃ 時，R1 的電阻剩下 34.6 Ω，因此 V_OUT 上的分壓變成：

V_OUT = 3.3*（34.6 /（34.6 + 220））= 0.45 V

假設 MCU 的 ADC 有 10 bit，那麽 25℃ 時的讀值就是：

1023 *（1.65/3.3）= 511

而 80℃ 時的讀值則是：

1023*（0.45 / 3.3）= 139

事實上這樣的做法有幾個問題。

首先是功耗。我們可以算一下，當溫度來到 80 ℃ 時，R1 跟 R2 整串的總電阻只有 34.6 + 220 = 254.6 Ω，以電源電壓 3.3 V 來計算，兩顆電阻上的總功耗就是：

P = V²/R = 3.3²/254.6 = 0.043 W

這個功率已經接近大部分 0603 電阻的功耗上限。雖然它是分在兩顆電阻上，但設計餘裕仍然太小，不是一個好設計。因此實務上這裡我們不會用常溫下阻值只有 220 Ω 的 NTC 熱敏電阻，而會用電阻更大的零件，如表中的 NCP18XW222，常溫下有 2.2 KΩ。

再來是 ADC 的範圍。如果我們只需要測量 25-80℃，上面這個電路並沒有完全地利用 MCU 的 ADC 範圍，因爲 R1 電阻最大時就是在 25℃，而此時 V_OUT 的電壓只有 1.65 V，隨著溫度越來越高， V_OUT 的電壓只會下降，因此我們浪費了 ADC 在 1.65 V 以上的測量範圍。

解決這個問題的方法，就是把 R2 改小，讓 NTC 熱敏電阻在室溫下時的電阻能造出盡量高的讀值。這樣做同時還能改善高溫時測量的解析度。由於 NTC 熱敏電阻的非線性特性，溫度越高時電阻的變化量會越小，因此若能把低溫時的讀值盡量拉高，高溫時就有更多的動態範圍可以使用。

當然，R2 改小的前提是 R1 要夠大，讓整體的功耗落在合理的範圍。

最後一個問題就是這整個測量系統的非線性。我們前面的計算都是用溫度來求得 NTC 熱敏電阻的阻值，但實務上如果拿它來測量溫度，我們是要測量它的電阻值，再換算出溫度。

記得我們剛剛在計算時用了自然對數底的冪次方 exp（）嗎？這表示反過來算時就要求自然對數底的對數。雖然標準 C 語言的數學函式庫裡有 log（）跟 log10（）這兩個標準函數，分別可以用來求以 e 爲底和以 10 為底的對數，但對於沒有浮點計算能力的小型 MCU 來説，算對數仍然是非常吃力且麻煩的事。

因此常用的做法就是查表。我們可以先把溫度對阻值的計算先用試算表之類的工具完成，再把它建成一個以阻值為 index 的常數陣列，就可以很簡單地用查表得方法換算這種非線性的方程式計算。查不到的值可以用相鄰兩個 index 來内插，精度也還可以。

小結

以上就是這次介紹的，關於用 NTC 熱敏電阻測量溫度的方法。由於這是類比的電路，在連接到 MCU 的 ADC 界面上還有一些不確定的因素如參考電壓、雜訊等問題需要處理，實際使用時可能還有校正的問題。

有沒有更簡單、更可靠的方法可以測量溫度呢？有！市面上其實有很多專門用來測量溫度的 IC，而且它們的輸出界面是數位的，完全沒有參考電壓、轉換、或是校正的問題。下回我們再來介紹這些專門用來測量溫度的 IC 以及它們的應用。

（責任編輯：賴佩萱）

• About
• Latest Posts

Liang Bird

在外商圈電子業中闖蕩多年，經歷過 NXP、Sony、Crossmatch 等企業，從事無線通訊、影像系統、手機、液晶面板、半導體、生物辨識等不同領域產品開發。熱愛學習新事物，協助新創團隊解決技術問題。台大農機系、台科大電子所畢業，熱愛賞鳥、演奏管風琴、大提琴、法國號，亦是不折不扣的熱血 maker。

Latest posts by Liang Bird (see all)

• 【Maker電子學】Flash 記憶體的原理與應用—PART22 - 2025/02/27
• 【Maker電子學】Flash 記憶體的原理與應用—PART21 - 2025/02/21
• 【Maker電子學】Flash 記憶體的原理與應用—PART20 - 2025/01/24