作者:Bird
上一回【Maker電子學】淺談高頻系統的原理與設計—PART6,我們利用實際的電路,示範如何用阻抗的複數座標系統來計算阻抗的角度所造成的電壓電流相位差,以及阻抗的大小所決定的峰值電流。
我們強調過,「阻抗」是由電阻和電抗兩個互相獨立的特性所組成。電阻與頻率無關,不管在什麼頻率,電阻的阻值都不會改變,但不管是電感性(j 爲正值)或電容性(j 爲負值)的電抗,在公式中都有 f 頻率這一項,表示感抗和容抗除了和電容值和電感值有關,也和頻率有關,因此整體的阻抗值也會和頻率相關。
這一回我們就要來看看「頻率」在交流電路中所扮演的角色。
隨頻率變化的阻抗 #
上一回我們看過這個電路:
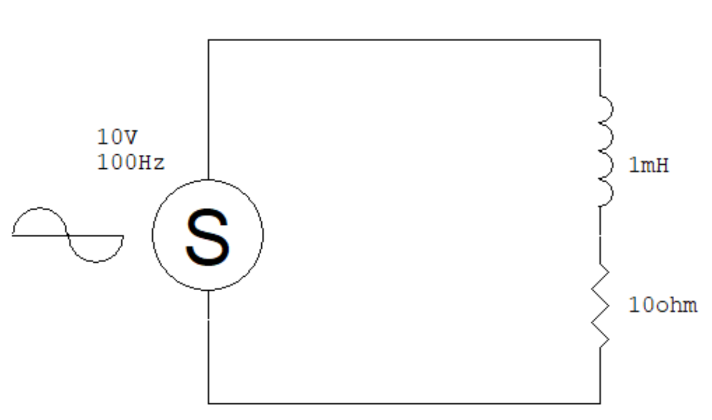
(圖片來源:Bird 提供)
這個電路中,電感和電阻加起來的阻抗就是:
Z = X + R = j 2𝝅fL + R = 6.28 *100*1* 0.001 + 10 = 0.628j + 10(ohm)
我們把這個結果畫到複數座標系上,看起來就是這個樣子:
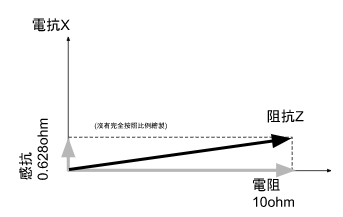
(圖片來源:Bird 提供)
這是電源爲 10 V 100 Hz 時的計算結果。如果電源的頻率變成 1 KHz 時,會發生什麼事呢?
由於電感的感抗是 j 2𝝅fL,當頻率變爲原來的 10 倍時,可以預期感抗也會變爲原來的 10 倍,因此在 1 KHz 時整個電路的阻抗就會是:
Z = X + R = j 2𝝅fL + R = 6.28 * 1000 * 1 * 0.001 + 10
= 6.28j + 10(ohm)
畫在複數座標系上,就會變成這個樣子:
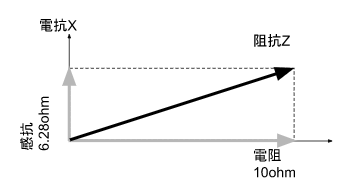
(圖片來源:Bird 提供)
因爲電抗改變了,阻抗的相位和大小也會跟著一起變。
相位,也就是它所造成的電壓、電流相位差,會變成:
𝜭 = arctan(X / R)= arctan(6.28 / 10)= 0.56(rad)= 32.12(度)
而阻抗的大小,或叫做「絕對值」,則會變成:
Zmagnitude = SQRT(R2+X2)= SQRT(10*10 + 6.28 * 6.28)= 11.808
我們繼續把電流波形和電壓波形畫在同一張圖上,看起來就是這樣:
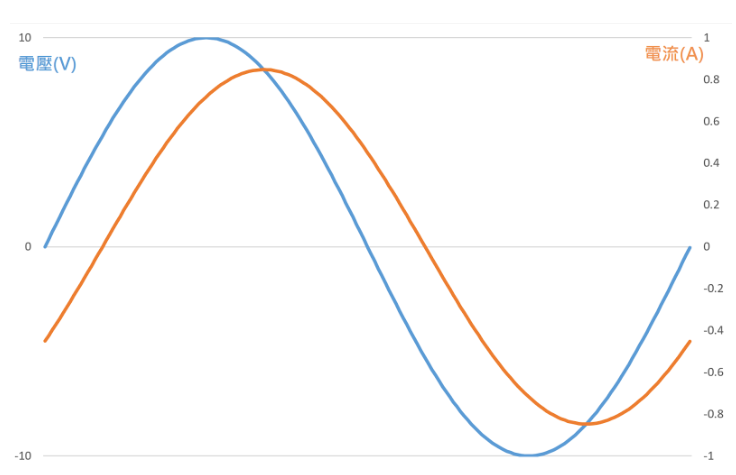
(圖片來源:Bird 提供)
注意,雖然我們只畫出一個週期,但此時頻率是原來的 10 倍,因此水平的時間刻度與上回的那張在 100 Hz 下畫出來的圖是不同的。
可以看出,當頻率變爲原來的 10 倍後,因爲感抗增加,電抗佔全體阻抗的部分也隨之增加,因此電感上電流落後電壓的相位差也跟著增加。上一回我們畫 100 Hz 的圖時,由於電流落後電壓的相位差只有 3.59 度,因此電壓與電流兩條線幾乎是重疊在一起的,但當頻率增加到 1 KHz 時,由於相位差變成 32 度,圖上兩條線也就明顯分開了。
當電壓與電流的相位越分越開,會發生什麼事呢?
能量的流動 #
功率是單位時間內的能量,根據功率的公式,P = I * V,我們把電壓和電流的數值逐點相乘後,就可以得到功率的曲線。把電壓、電流、功率三條線畫在同一張圖上,我們可以得到這樣的圖:
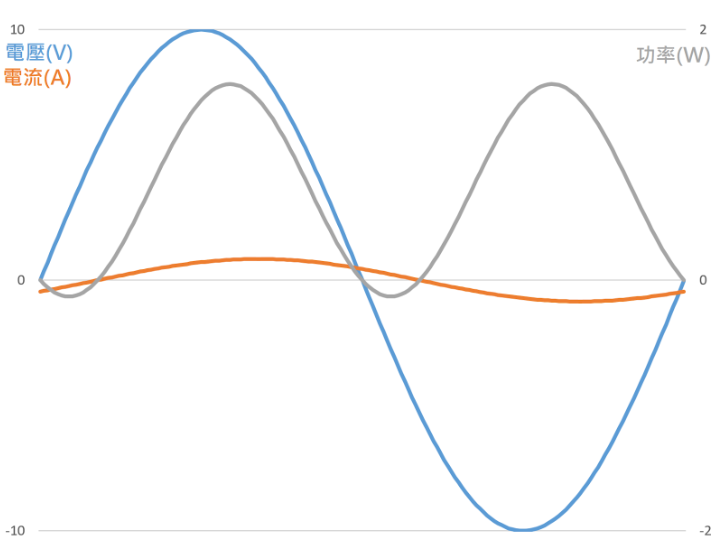
(圖片來源:Bird 提供)
這是一張很妙的圖,電壓、電流、功率三個週期波形的相位都不一樣,也就是說他們的峰值位置都不一樣,而且你有沒有注意到,功率的曲線某些時候會在 0 以下,也就是負的。
負的功率代表能量的流動方向反過來:由負載流向電源。
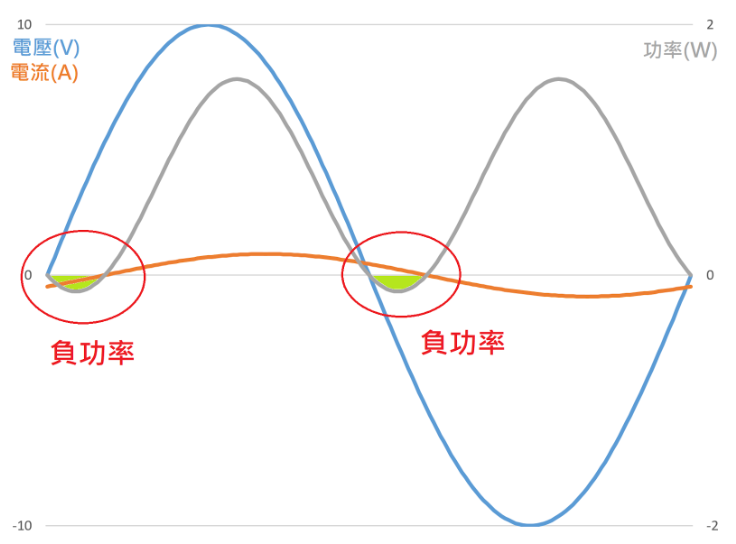
(圖片來源:Bird 提供)
我們在前幾回討論純電感或純電容的阻抗時,有看過類似的現象:電感和電容在交流電路中不消耗功率;它們會儲存能量,然後把能量再吐回去給電源。當電路中有電抗存在時,因爲會造成電壓和電流的相位差,當電壓和電流的符號不同時,乘起來的功率就會是負的,也就是能量逆流的時候。
在大部分的情況下,我們都希望能量盡可能的從電源傳遞到負載,而不是送到負載後又被吐回去給電源,但當負載有電容或電感時,因爲電流和電壓會有相位差,一定會有這種「做白工」的現象,這在交流電路中叫做「虛功」。
有沒有辦法解決這個問題呢?有。我們前面說過,電抗分成感抗和容抗兩種特性,它們不會同時存在,而會互相抵消。感抗的 j 項是正的,而容抗的 j 項是負的。
在上面那個例子中,當頻率是 1 KHz 時,負載的電抗是 6.28 j。如果我們找個電容器串在電路上,而且這個電容器的電抗在 1 KHz 時是 -6.28 j 的話,不久可以抵消電感的感抗了嗎?
根據容抗的公式 XC= -1 / 2𝝅fCj,我們現在要求一個 C 使它的 XC 在 1KHz 時等於 -6.28 j。
-6.28 = -1 /(2𝝅 *1000*C)
C = 2.5356 * 10^-5(F)= 25.356(uF)
讓我們把這個電容放到電路裡面,變成這樣:
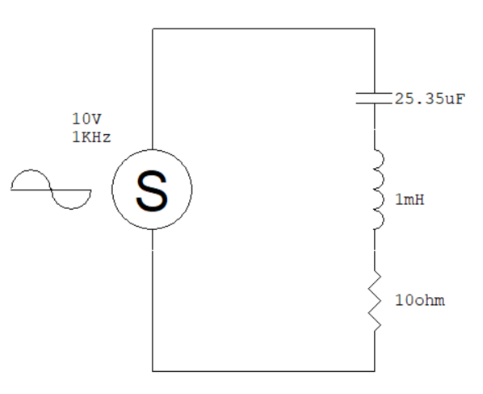
(圖片來源:Bird 提供)
這個負載的阻抗就變成:
Z = X + R = XC + XR + R = -1 /(2𝝅fCj)+ 2𝝅fLj + R = -6.28j + 6.28j + 10 = 10(ohm)
很神奇地,電感和電容的電抗互相抵消掉了。這個電路中雖然有電感也有電容,但最後整體的特性只剩下一個 10 ohm 的電阻,電流和電壓也不再有相位差。在交流電力的輸配電工程中,常常利用這樣的技術,讓電感性的負載加上電容器,使它們總和的特性接近電阻性,來改善能量傳遞的效率,儘量不要做白工。
但這裡還有一個難題:依舊是頻率。我們剛剛計算用來抵消電感感抗的電容器數值時,是用 1 KHz 的電源頻率來計算。如果電源頻率不是 1 KHz 呢?同樣的電路會變成什麼樣子?
我們把電路中的電抗部分單獨拉出來計算,並將頻率 f 當作變數:
XC + XR = -1 /(2𝝅fCj)+ 2𝝅fLj
接著我們把容抗、感抗和總電抗在 100 Hz 到 2 KHz 這個區間的曲線畫出來,會得到一張這樣的圖:
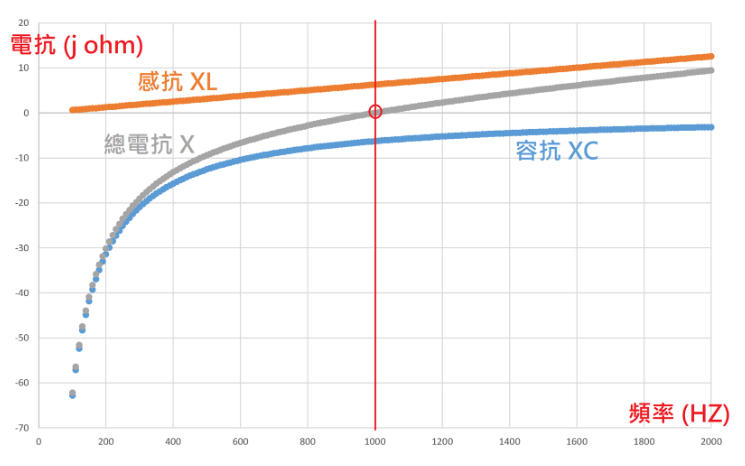
(圖片來源:Bird 提供)
由於容抗的頻率項 f 在分母,因此容抗對頻率的函數畫出來會是一條雙曲線,也就是上圖中淺藍色的線,而感抗的頻率項 f 在分子,因此感抗對頻率的函數就是個線性函數,也就是上圖中橘色的線。
觀察從 100 Hz 到 2000 Hz 的曲線,我們可以發現,在 1000 Hz 以下時,總電抗是負的,也就是說這個負載在 1000 Hz 以下時是電容性的,它的電流會超前電壓;在 1000 Hz 時,感抗和容抗的大小剛好相同、符號相反,因此兩種互相抵消,就如同我們前面計算過的一樣,此時這個負載會是純電阻性的,沒有電抗,電流與電壓同相位;當電源頻率超過 1000 Hz 以上時,感抗會大於容抗,因此總電抗是正的,也就是說這個負載在 1000 Hz 以上時是電感性的,它的電流會落後電壓。
由於容抗與感抗的公式不同,一個是雙曲線函數、一個是線性函數,在頻率變化時兩者的變化趨勢並不相同,這也造成了交流電路在頻率變化時,特性會有很大的變化。從上圖也可以看出來,在頻率很高時,容抗的減小很有限,但感抗的增加卻會隨著頻率的增加一去不回頭。
小結 #
這一回我們探討了交流電路中,容抗與感抗隨著頻率變化的現象,並介紹了可以讓兩者在特定頻率互相抵消的電路與計算。
下一回我們要開始進入高頻電路中比較複雜的阻抗觀念,並繼續探討實作上一些有用的工具。
(責任編輯:賴佩萱)


