作者:Bird
上一篇文章我們介紹了「阻抗」在直流電系統中的定義,也談了「電阻」以及它在直流電路中的效應。
在交流甚至高頻的系統,阻抗不只是電阻,它還有電容與電感的特性,因此在交流系統中的阻抗要用數學中的複數系統來標示。同樣的,交流系統中的電壓與電流在電容與電感存在時,也會產生相位上的差異,因此交流系統中的電壓與電流也需要用複數系統來表示與計算。
這一回我們要來探討一下「阻抗」在交流系統中的作用。
先從簡單的開始 #
我們先從電阻開始,看一個簡單的電路。
上一回我們用的 power source 是一個直流電壓源,這一次我們要使用交流電源。假設有一個峰值電壓 10 V、頻率 100 Hz 的交流電源,我們將它接上一個 1 ohm 的電阻當作負載。這個電路就會長這樣:
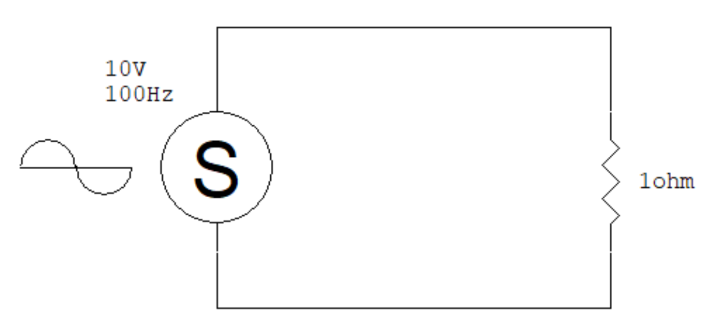
(圖片來源:Bird 提供)
所謂的「100 Hz」交流電源,指的一定是 100 Hz 的正弦波,而不是方波、三角波、階梯波或是任何其它的波形。傅立葉分析告訴我們,任何形狀的週期波都可以用不同頻率的正弦波疊加而成,因此當我們在探討單一頻率的波形時,講的一定是正弦波。
這個交流電壓源的電壓波形就會長這樣:
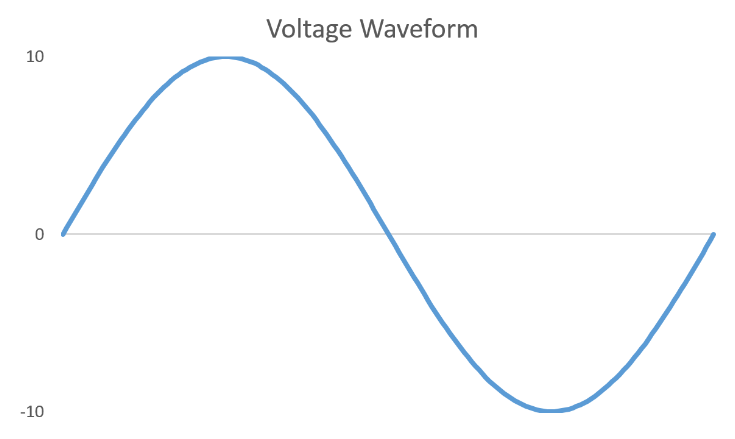
(圖片來源:Bird 提供)
那麼電流呢?我們上一次討論過,如果電源是個電壓源,要流出多少電流是由負載的電阻大小決定的,而對於一個會變動的電壓源來說,即使它輸出的電壓在變動,它也時時刻刻遵守這個定律,也就是我們熟知的歐姆定律:V = IR。
當電壓爲 0 時,我們將電壓(0 V)和負載(1 ohm)帶入上式,就會知道電流也是 0;當電壓上升到 5 V 時,我們將電壓(5 V)和負載(1 ohm)帶入上式,可以得知電流是 5 A;當電壓上升到頂點 10 V 時,我們將電壓(10 V)和負載(1 ohm) 帶入上式,就可以得知電流是 10 A。
然後有趣的事來了。由於這個電源是交流電,它的電壓在整個週期中有一半的時間會低於 0,因此當我們把小於 0 的電壓帶入上面的式子計算時,電流也會小於 0;當電壓是 -5 V 時,電流是 -5 A;當電壓是 -10 V 時,電流是 -10 A。
電流的符號代表它流動的方向,如果我們定義電流由上往下流動是正的,那麼當電壓變爲負的時候,電流就會由下往上流動。
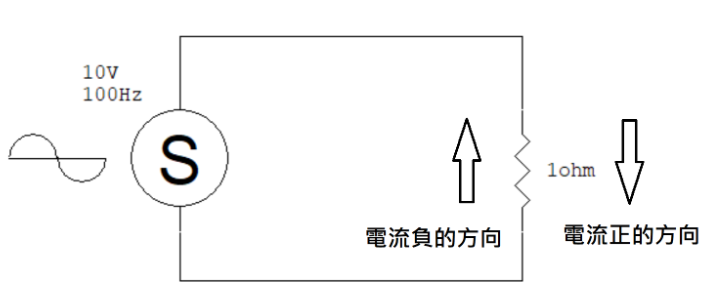
(圖片來源:Bird 提供)
如果我們把電流波形畫出來,就會是看起來就會是這樣:
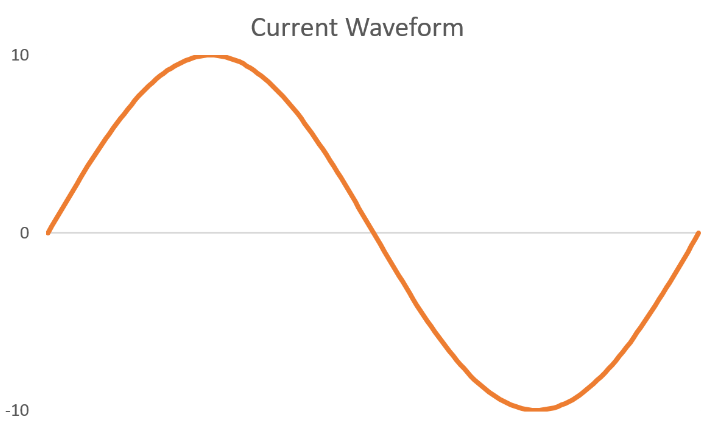
(圖片來源:Bird 提供)
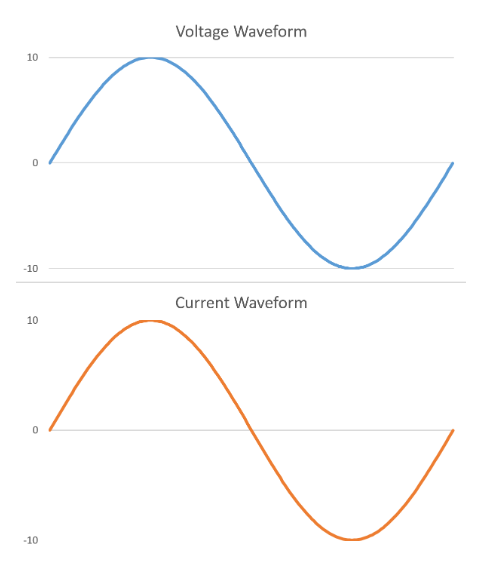
如果我們把電壓波形和電流波形的時間軸對齊畫在一起,看起來就會是這樣:
(圖片來源:Bird 提供)
電流波形會隨著電壓的變化從 0 開始上升到最高點,再下降回到 0,然後變成負的,再到最低點,最後回到 0,如此周而復始。
由於電流波形很精確地隨著電壓波形變化,同時出發、同時達到最高點、同時達到最低點,因此我們說在這個電路中,電壓波形與電流波形的相位相同。
電容器負載 #
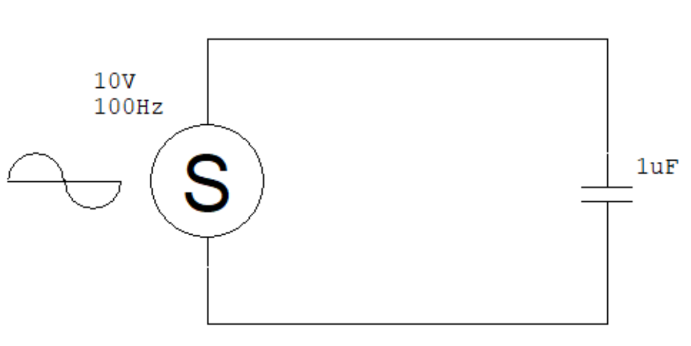
如果我們將上面電路中的負載電阻換成一個 1 uF 的電容器,會發生什麼事呢?這時電路會變成這樣:
(圖片來源:Bird 提供)
再次強調,由於電源是個電壓源,電壓波形由它自己決定,而電流波形則由負載決定,也就是說,電壓是因,電流是果。
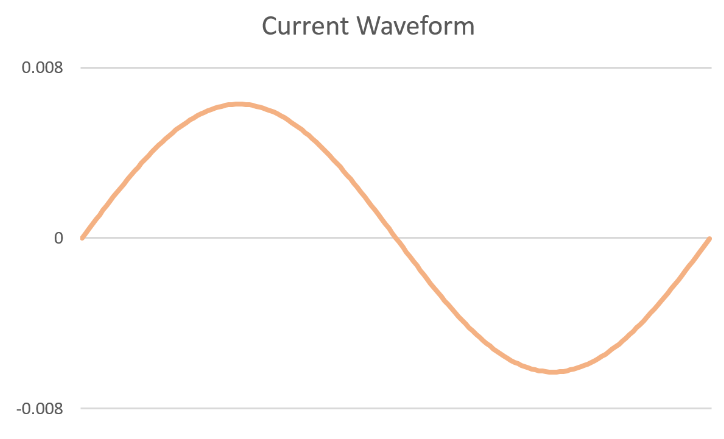
如果我們測量這個電路的電流波形,它會是這樣:
(圖片來源:Bird 提供)
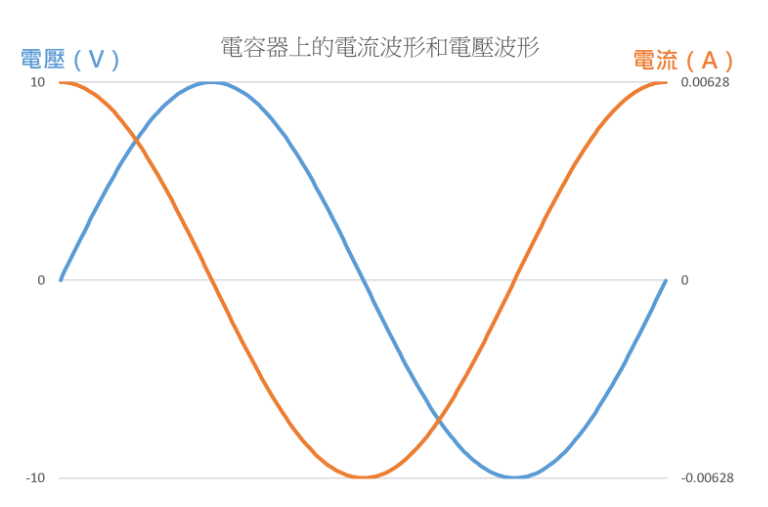
看起來仍然是個正弦波,沒什麼特別的,除了垂直刻度稍微怪了一點,但如果我們同時將電壓波形和電流波形畫在同一個時間軸上的話,就會是這樣:
(圖片來源:Bird 提供)
原來在交流電路中,電容器上的的電流和電壓會有時間差。從這個圖中看起來,電容器上的電流會比電壓先上升到最大值,因此我們說電容器上的電流相位「超前」電壓,或是電壓相位「落後」電流。
至於超前或落後多少,其實可以很容易從圖中看出來,剛好就是四分之一個正弦波的週期。如果用角度來計算,一個週期是 360 度,四分之一個週期就是 90 度。因此我們可以這樣說:在交流電路中,電流相位超前電壓相位 90 度。
相位差知道之後,我們再來看振幅。眼尖的讀者可能已經看到,我雖然把電壓和電流畫得一樣高,但其實它們的座標軸不一樣。電壓的頂點依舊是 10 V,但電流的頂點只有 0.00628 A。這個 0.00628 A 是怎麼來的呢?
電容有個公式叫做它的容抗,我們在以前的文章中偶爾會用到它:XC = 1 / 2𝝅fC。
這個公式算出來的答案,單位是歐姆。換句話說,電容器在這個交流電路中,也像個電阻一樣,可以決定特定的電壓流過多少電流,只不過電流的相位會跟電壓差 90 度。
而有趣的是,這個公式中有一項 f 代表頻率,也就是說電容器所表現出來的容抗,會與加在它上面的交流電頻率有關。由於頻率項在分母,因此 f 越大,算出來的容抗就越小。電容量這一項本身也在分母,因此電容器越大,在特定頻率的容抗也會越小。
由於 f 項在分母,如果頻率等於 0,不管電容多大多小,算出來的容抗都是無限大。頻率等於 0 的訊號就是直流電,因此對直流電來說,電容器的容抗是無限大的,也就是說直流訊號是過不了電容器的。
以上面那個電路來說,頻率是 100 Hz,電容是 1uF(1 乘以 10 的負 6 次方 F),我們就可以算出電路中的容抗是:XC = 1 / 2 * 3.14 * 100 * 0.000001 = 1 / 0.000628 = 1592(ohm)。
換句話說,撇開相位的差異不談,電容器在這個電路中的等效電阻是 1592 ohm。以頂點的電壓 10V 來計算,套用歐姆定律 V = IR,我們可以算出頂點的電流是:10(V)/ 1592(ohm)= 0.00628(A)。
現在我們知道這個 0.00628 A 是怎麼來的了。
電感負載 #
如果我們將上面電路中的負載電阻換成一個 1 mH 的電感,會發生什麼事呢?這時電路會變成這樣:
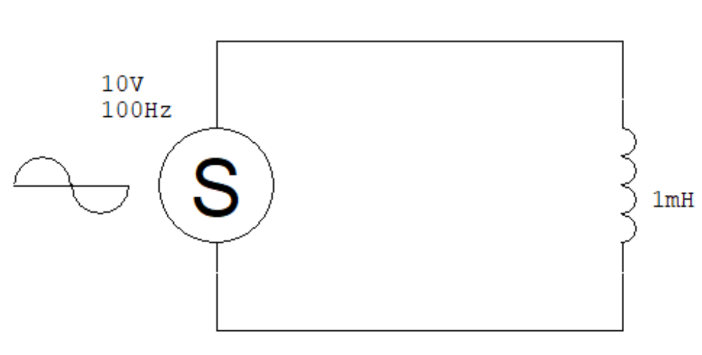
(圖片來源:Bird 提供)
聰明的讀者可能已經猜到,電感也會在交流電路中造成電壓與電流的相位差。而且由於物理學上有許多美妙的對稱性,電感在交流電路中的電壓與電流波形會是這樣:
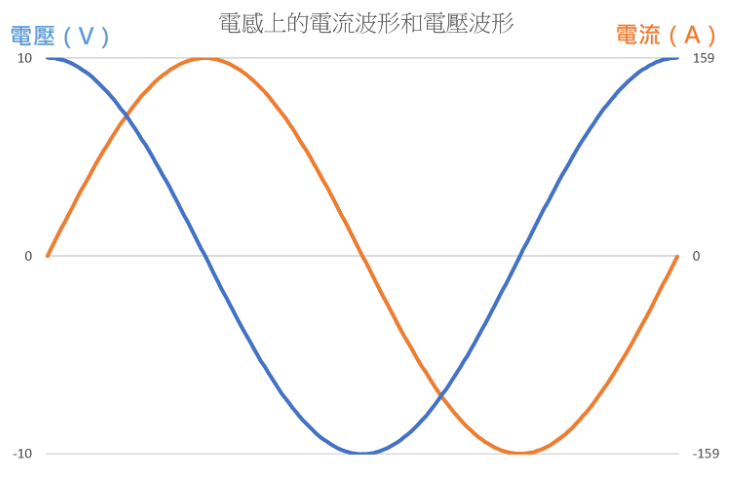
(圖片來源:Bird 提供)
可以看到,隨著時間的流逝,電感上的電壓先上升到頂點,電流隨即才跟著上升到頂點。電感上的電流波形總是比電壓波形慢一點,大約慢四分之一個弦波週期,90 度。至於電感上的電流大小,和電容器一樣,也有一個叫做「感抗」的特性可以計算。感抗的公式:XL = 2𝝅fL。
這次沒有人在分母了。從公式可以看出來,頻率越高,感抗越大;電感越大,感抗也越大。我們一樣來算算看這個電路中電感的感抗:XL = 2 * 3.14 * 100 * 0.001 = 0.628(ohm),再套用歐姆定律,我們就可以算出電感上的最大電流:10(V) / 0.628(ohm)= 159(A)。
嗯,當然前提是這個 10 V、100 Hz 的交流電源要能吐得出 159 A 這麼大的電流啦…
小結 #
這一回,我們說明了在交流電路中,電容和電感的電壓波形與電流波形,並說明了「容抗」與「感抗」的公式。由於電容電感在交流電路中都會造成電壓與電流的相位差,因此最大的電壓與最大的電流並非同時發生,但我們仍然可以套用歐姆定律來計算最大的電流。
事實上我們今天用來計算容抗與感抗的公式仍然稍微簡化了一點。下一回我們要繼續探討容抗與感抗的觀念,並將電流與電壓的相位差也納入計算公式中。
(責任編輯:賴佩萱)


