作者:Bird
上一回【Maker電子學】淺談高頻系統的原理與設計—PART20:史密斯圖(6),我們看了在 online Smith Chart 中,當 frequency span 不爲 0 時,計算出來的終點會有什麼變化。我們也介紹了 S11 參數,並看了之前算出來的兩組解,它們的 S11 參數在不同頻率之間的差異。
這一回我們會繼續介紹設計阻抗匹配電路時,零件數值與匹配結果之間的關係。
電容與電感 #
我們前兩回設計了兩組解,將特性阻抗爲 39+6j 的一個黑盒子匹配到 50 ohm 的目標阻抗。第一組解是先串聯 2.4 pF、再並聯 6 nH 電感;第二組解則是先串聯 0.9 nH 的電感、再並聯 0.7 pF 的電容。
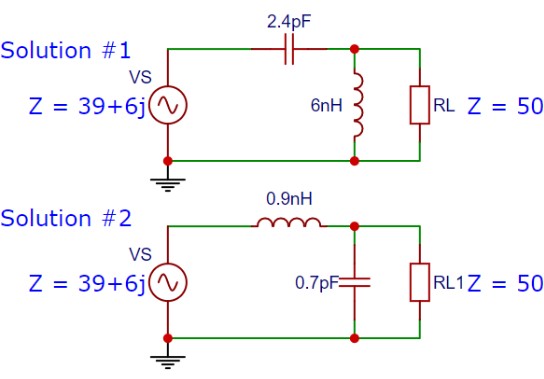
(圖片來源:Bird 提供)
上一回我們用 Online Smith Chart 模擬兩組解在整個 2400 MHz – 2500 MHz 頻段中的表現時,發現第一組解的最佳工作點,也就是最匹配時的 S11 參數大概在 -56 dB,比第二組解的 -37 dB 要好,但是第一組解在整個頻段中的均勻度並不好,最差和最好的地方相差了 15 dB 左右,而第二組解在整個頻段中的均勻度則相對平坦,整體的差距在 1 dB 以內。
會造成這樣差距的原因有很多,但是其中一個很重要的因素是零件的數值大小。
由於電感和電容的電抗都是頻率的參數:
XL = j 2 𝝅 f L
Xc = 1 /(j 2 𝝅 f C)
在零件數值不變的狀況下,頻率越高,感抗越大、容抗越小,而由於容抗和感抗都是經由零件數值與頻率相乘計算出來的,在同樣的頻率變化範圍下,電感的數值越大,感抗的變化量就越大,而電容的數值越大,容抗的變化量也就越小(因爲容抗的 C 項在分母)。
因此我們可以預期,在頻率從 2400 MHz 變化到 2500 MHz 這樣的範圍中,一個 10 nH 電感的感抗變化量,一定比一個 1 nH 電感的容抗變化量要大。
但事情比這個再稍微複雜一點,因爲我們使用電感和電容來做阻抗匹配時,有串聯和並聯兩種接法。
串聯電路 #
我們先來看串聯。爲了讓 Smith Chart 上 frequency span 造成的效果比較明顯易讀,我們將中心頻率設爲 3 GHz,span 設爲 +/- 1 GHz。
然後我們直接在 50 ohm 的 source 上串聯一個 10 nH 的電感,看看阻抗會偏移到哪裡:
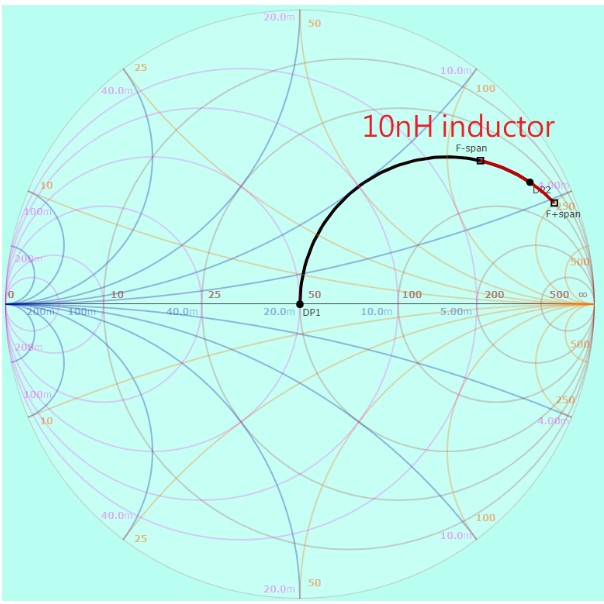
(圖片來源:Bird 提供)
黑色線段尾端的紅色線段,就是在整個 3 GHz +/- 1 GHz 的頻段中,10 nH 電感所造成的最終阻抗,而紅色線段中間的黑色圓點就是中心頻率 3 GHz 時的特性阻抗。由於 Smith Chart 中的刻度不是線性的,所以中心頻率的阻抗並不會位在紅色線段的正中間。
現在我們將電感改成 1 nH,看看阻抗變成什麼樣子:
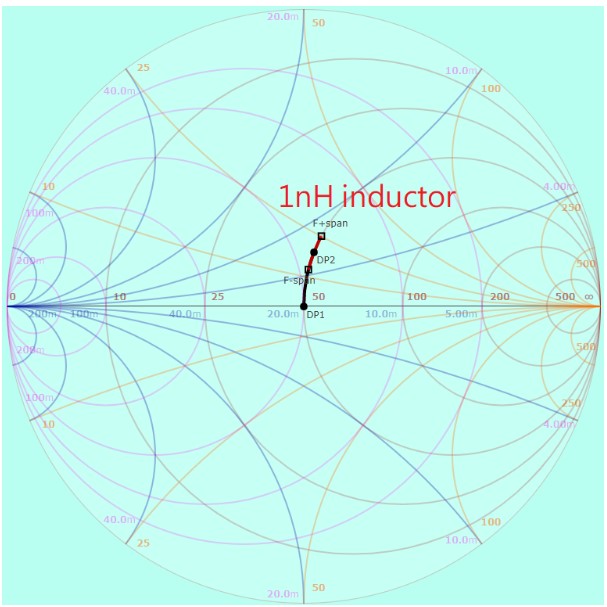
(圖片來源:Bird 提供)
可以看到當串聯電感變成原來的十分之一時,紅色線段的長度也變得比較短了。前面說過,Smith Chart 的刻度不是線性的,所以不能直接比較圖上的距離,而要看刻度。
我們放的這兩個電感,都會讓阻抗沿著 50 ohm 的等電阻圓移動,它們造成的是電抗部分的改變,因此我們可以看 Smith Chart 中的橘色刻度來判斷各點的電抗。10 nH 電感在 3 GHz +/- 1 GHz 頻寬中造成的電抗改變大概是 120 j 到 250 j,變化量有 130 j,而 1 nH 電感在這個頻寬中造成的電抗改變則大概從 12 j 到 25 j,變化量約 13 j(因爲電抗的公式是線性的,這個結果是可以預期的)。
現在我們來看串聯電容。我們用一樣的頻率範圍設定,比較串聯 1 pF 和 10 pF 電容所造成的結果:
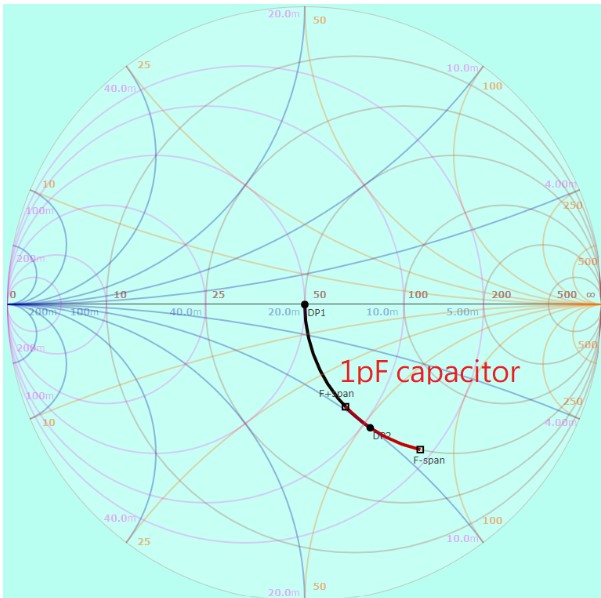
(圖片來源:Bird 提供)

(圖片來源:Bird 提供)
由於容抗是負的,串聯電容會讓電抗減少,因此曲線會往 Smith Chart 的下方走。比較這兩張圖,我們會發現,串聯電容時,在同樣的頻率變化範圍內,較大的電容反而會造成較小的變化量。這也是可以預期的,因爲電容的電抗公式中,C 項在分母。
那麼並聯呢?
並聯電路 #
我們直接來模擬看看好了。我們用同樣的頻率範圍,分別放置 1 nH 跟 10 nH 的並聯電感,看看最後的線條會變成什麼樣子:
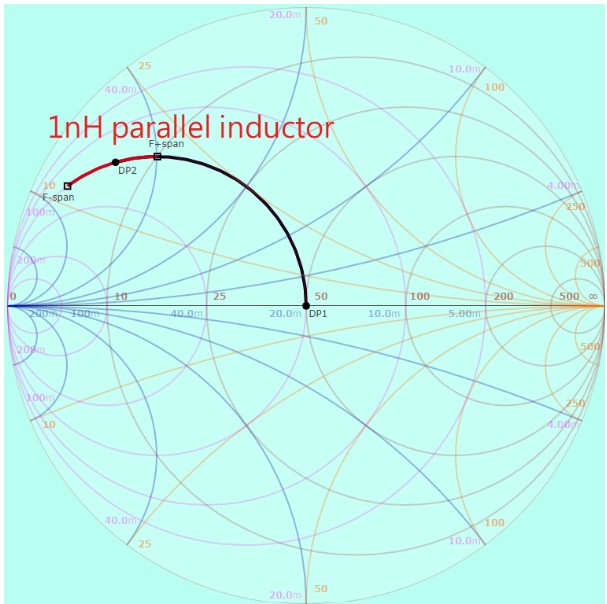
(圖片來源:Bird 提供)

(圖片來源:Bird 提供)
由於並聯電路的電阻和電抗都要取倒數後相加再取倒數,很難計算,所以我們之前在手動計算時介紹過,並聯電路都會轉換到導納的領域來計算。串聯是阻抗相加,並聯就是導納相加,因此當我們在電路中並聯電感時,圖中的特性阻抗會沿著等電導圓移動,我們從 50 ohm 的標準特性阻抗出發,而 50 ohm 換算成電導就是 0.02 Siemens:
1 / 50(ohm)= 0.02(Siemens)
所以當我們並聯電感時,上圖中的曲線會從 0.02 + 0j Siemens 的點出發,沿著 0.02 Siemens 的等電導圓向上移動。
我們發現,在同樣頻率變動範圍中,並聯 10 nH 電感所造成的阻抗變化,比並聯 1 nH 電感要小,這結果似乎跟串聯電感時相反。
這是因爲並聯時,我們計算的是導納,而導納是阻抗的倒數;換句話說,本來電感在串聯時造成的變化量在分子,在並聯時跑到了分母,因此電感越大、電納反而越小,所以這個結果是可以預期的,也符合邏輯的。
那並聯電容呢?聰明的讀者一定猜到了,電容的電納是電抗的倒數,而電容的電抗公式中 C 項在分母,再經過一次倒數計算後 C 項就跑到了分子。電容和電感的電納公式是這樣(這個式子超少見到,所以還是讓它曝光一下好了…)
BC = j 2 𝝅 f C
BL = 1 /( j 2 𝝅 f L)
所以我們可以預期,在同樣頻率變動範圍中,並聯 10 pF 電容所造成的阻抗變化,要比並聯 1 pF 所造成的阻抗變化要大,至於 Smith Chart 上的線段,就留給讀者們自己去畫畫看了。
綜合以上四種組合的嘗試:串聯電感、串聯電容、並聯電感、並聯電容,我們可以得到一個結論:在同樣的頻率範圍變化下,串聯電感越小、串聯電容越大,所造成的阻抗變化量就越小;並聯電感越大,並聯電容越小,所造成的導納變化量就越小。
知道這個關係後,我們在尋找阻抗匹配的解時,就可以比較了解零件數值的大小對最終結果的偏移量所造成的影響。
如果我們設計的電路只針對單一頻率,那也許不管零件數值的大小,各種解可能都可以匹配到目標阻抗,但現今的無線電系統通常都有一定的頻寬,如何在整個工作頻段內維持整個阻抗匹配電路都有效的工作,才是設計上真正挑戰的地方。
小結 #
這一回我們利用 Smith Chart 上 frequency span 的功能,模擬了不同零件數值大小對匹配結果的偏移量所造成的影響。串聯電路比較直覺,而並聯電路由於需要轉換到導納領域計算,稍微沒有那麼直覺,但結果仍然具有數學上的對稱性,可以理解。
下一回我們要繼續研究,當零件的數值決定後,如何選擇實體的電容、電感元件。這些元件除了電容量、電感量之外,還有哪些特性需要考慮的。
(責任編輯:賴佩萱)


