作者:Bird
在上一回【Maker電子學】淺談高頻系統的原理與設計—PART17:史密斯圖(3) 中,我們說明了用來阻抗匹配的四種電路:串並聯電感與電容,以及它們各自在 Smith Chart 上面對阻抗點造成的影響,最後也說明了定量的計算方法,以及頻率在整個計算中的關鍵角色。
這一回我們要以一個實際的例子,來帶大家走一次完整的計算流程。
命題 #
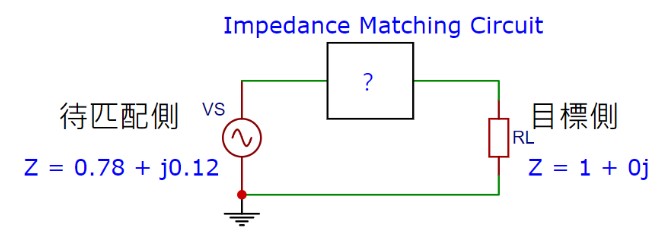
我們還是用之前 ESP8266 的那個例子。假設我們現在有一個 RF 晶片的輸出接腳,特性阻抗是 Z = 39 + j6,我們要如何設計阻抗匹配的電路,讓它能與 Z = 50 的天線或是連接器匹配呢?
因爲我們用的計算工具都是以正規化阻抗爲基準,因此我們先以 50 ohm 的目標阻抗,將這個題目正規化,變成 Z = 0.78 + j0.12。
接下來,我們就要透過電路,將這個阻抗變成 Z = 1 的目標阻抗。
(圖片來源:Bird 提供)
畫圖 #
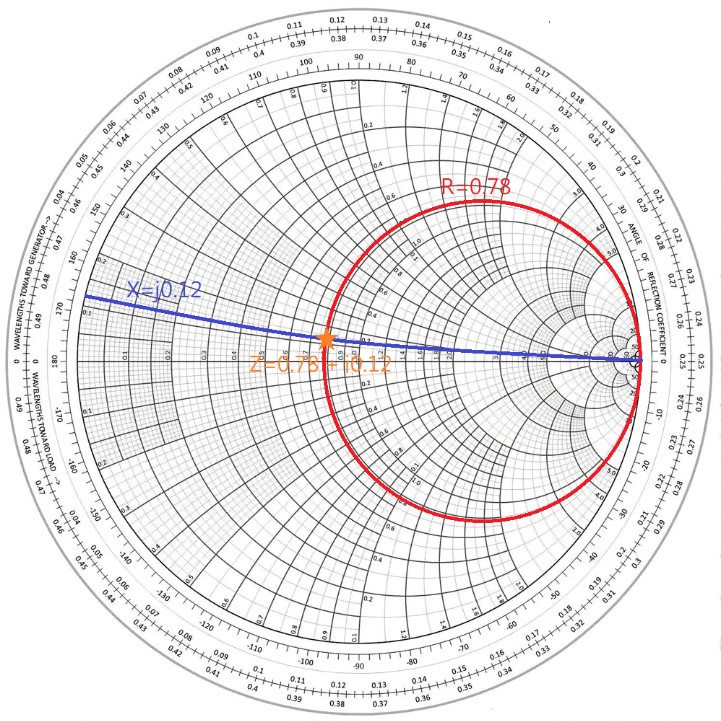
我們先在 Smith Chart 上把 Z = 0.78 + j0.12 這個點畫出來:
(圖片來源:Bird 提供)
在整張的 Smith Chart 上不太容易看出來這個點在哪裡,我們將它放大一點來看:
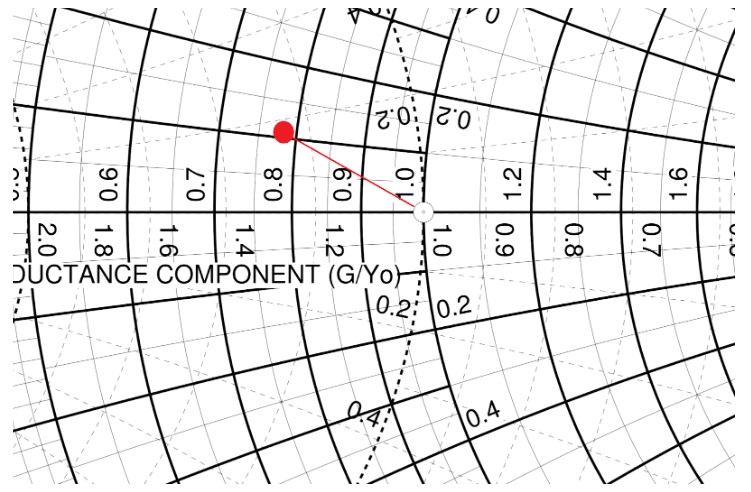
(圖片來源:Bird 提供)
上圖中紅色的圈圈就是 Z = 0.78 + j0.12 這個點,我們需要透過匹配的電路將它移動到圖中白色的圓圈處,也就是 Z = 1 + j0 的位置。
上一回我們說過,總共有四種電路可以用來改變阻抗,在 Smith Chart 上移動阻抗的位置:
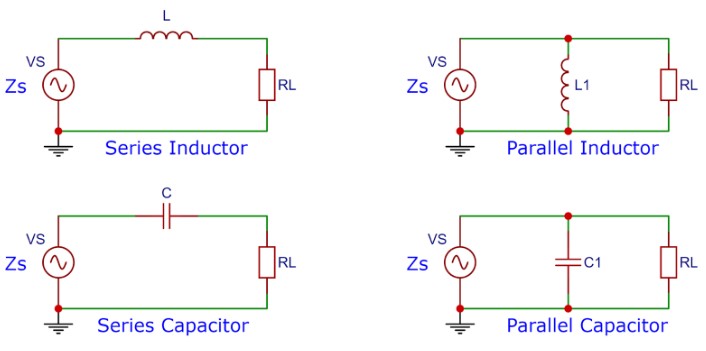
(圖片來源:Bird 提供)
這四種電路在 Smith Chart 上各自會沿著等電阻圓與等電導圓順時針、逆時針移動:
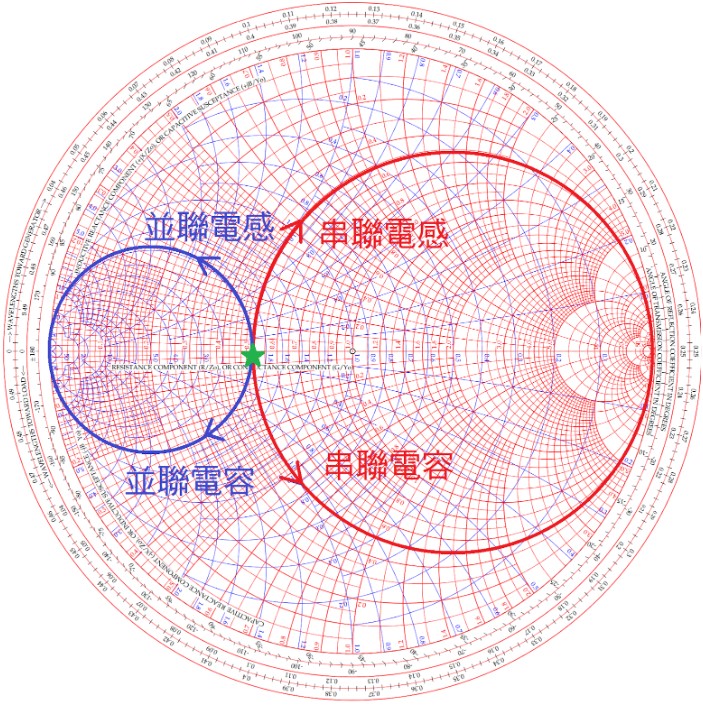
(圖片來源:Bird 提供)
整理一下:
- 並聯電感 – 等電導圓,逆時針
- 並聯電容 – 等電導圓,順時針
- 串聯電感 – 等電阻圓,順時針
- 串聯電容 – 等電阻圓,逆時針
等電阻圓是 Z Smith Chart 上的圓,而等電導圓則上 Y Smith Chart 上的圓,由於我們兩種圓都會用到,因此在用 Smith Chart 做阻抗匹配計算時,通常都會用阻抗與導納座標二合一的 Z-Y Smith Chart 來計算。
在圖上移動 #
我們用的 Smith Chart 刻度是 0.1,爲了方便接下來的計算,我們把命題四捨五入到最接近的刻度,變成 Z = 0.8 + 0.1j。將這個阻抗在 Z-Y Smith Chart 上畫出來:
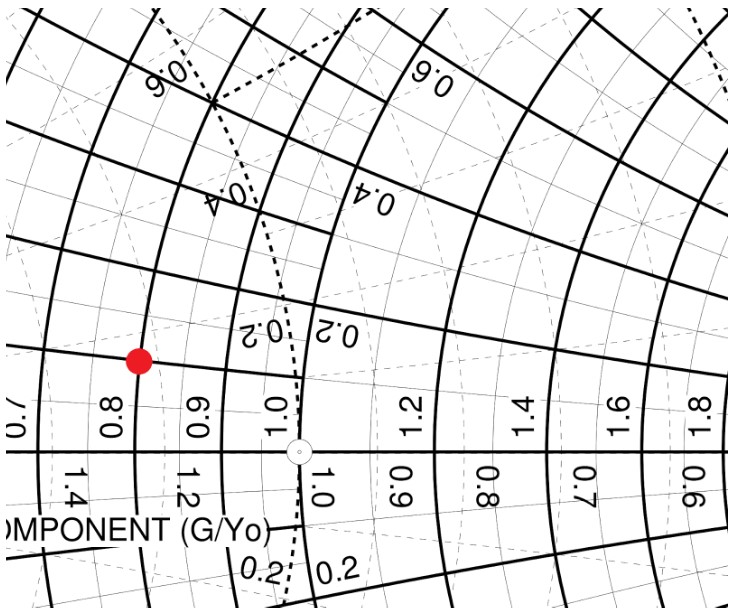
(圖片來源:Bird 提供)
上圖中的實線就是 Z Smith Chart,虛線則是 Y Smith Chart。當我們並聯電感或電容時,在圖上就會沿著虛線移動,而串聯電感或電容時,在圖上則會沿著實線移動。
現在我們的目的,就是要利用圖上的兩種圓弧,找出一條路徑,將紅色的點移動到中央的白色圓圈中。
要怎麼找出這條路徑呢?一個很常用的做法是:先看看來源阻抗與目標阻抗各自處在什麼等電阻圓或是等電納圓上,再找到這兩個圓的交會點,就可以形成一條路徑。
以這個題目來說,Z = 0.8 + j0.1(記得我們已經四捨五入了吧?),這個點位在 Z = 0.8 的等電阻圓上,而目標阻抗 Z = 1 則位在 Y = 1 的等電導圓上:
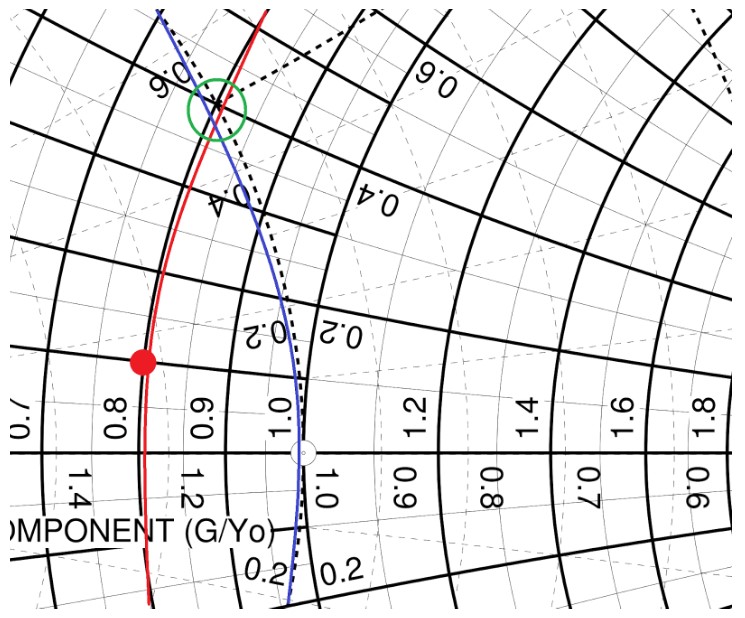
(圖片來源:Bird 提供)
這兩個圓則在 Z = 0.8 + j0.4 這個點上相交,且這個點同時也是導納 Smith Chart 上的 Y = 1.0 + j0.5 這個點。
於是我們就找到一條路徑了:可以先利用一個串聯電感,將 Z = 0.8 + j0.1 移動到 Z = 0.8 + j0.4,也就是 Y = 1.0 + j0.5,然後再利用一個並聯電容,將 Y = 1.0 + j0.5 移動到 Y = 1.0,也就是 Z = 1.0 的目標阻抗上。
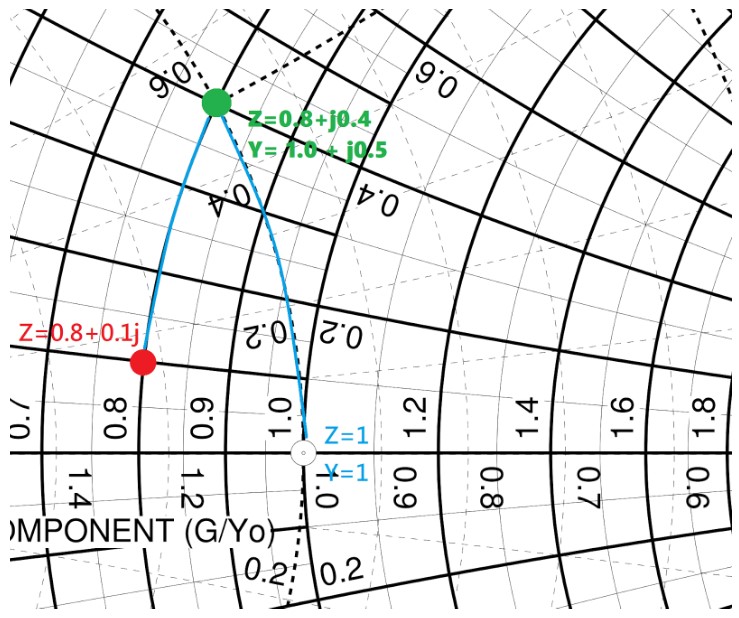
(圖片來源:Bird 提供)
要串聯多大的電感,才能將 Z = 0.8 + j0.1 變成 Z = 0.8 + j0.1 呢?我們需要增加 Z = j0.3 的電抗,換算回實際的阻抗就算 Z = j 15 ohm。
我們已經知道這個系統的工作頻率是 2.4 GHz,就以 2.4 GHz band 的中心頻率 2.45 GHz 來計算好了。電感的阻抗是:
ZL = j2𝜋fL
15 = 6.28 * 2450000000 * L
可以算出 L = 9.75 * 10^-10,單位是亨利(Henry),也可以寫成 0.975 nH。
接下來我們要並聯一個電容,讓 Y = 1.0 + j0.5 變成 Y =1.0,也就是說我們要減少 Y =j0.5 的電納。
由於我們熟悉的電容容抗公式是是用電抗而非電納來計算,因此我們先把 Y = j0.5 的正規化電納換算回正規化電抗,再換算回實際的電抗:
Z = 1 / Y = 1 / 0.5 = 2(正規化電抗)
Zactual = 2 * 50 = 100(ohm)
好,我們需要一個在 2.45 GHz 頻率下,電抗爲 100 ohm 的電容。
ZC = 1 / (j2𝜋fC)
100 = 1 /(6.28 * 2450000000 * C)
可以算出 C = 6.5 * 10^-13,單位是法拉(Farad),也可以寫成 0.65 pF。
整理一下,電路就變成這個樣子:
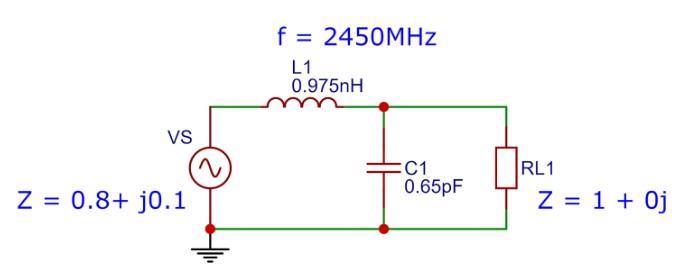
(圖片來源:Bird 提供)
於是我們成功地利用一個串聯電感和一個並聯電容,將 Z = 0.8 + j0.1 的特性阻抗,匹配到 Z = 1 + 0j 的目標特性阻抗了。
阻抗匹配的解答不是唯一的,當我們知道如何利用零件在 Smith Chart 上任意移動之後,我們可以找出非常多條路徑前往目標特性阻抗。以這個例子來說,我們先用串聯電感將來源阻抗沿著等電阻圓往圖的上方移動,但我們也可以換一個做法:先利用串聯電容將來源阻抗沿著等電阻圓往圖的下方移動,再利用並聯電感往目標阻抗前進:
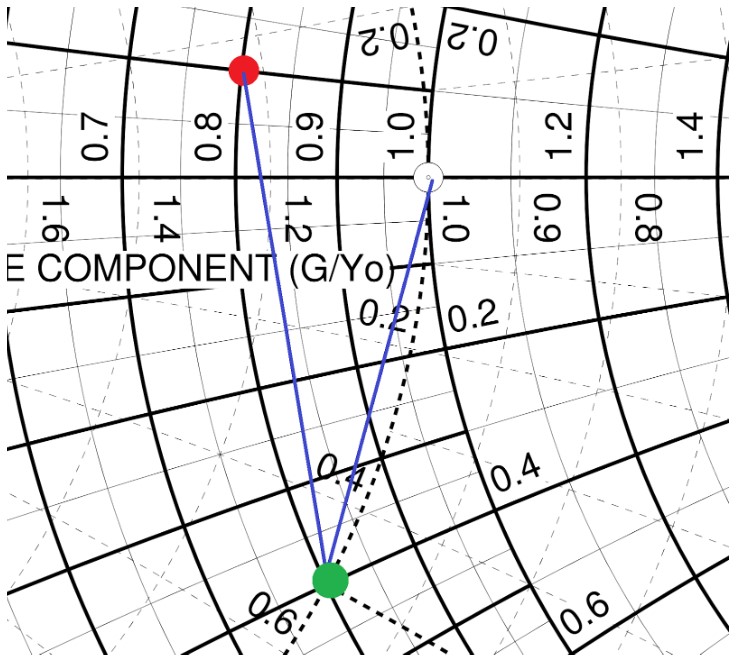
(圖片來源:Bird 提供)
在大部分的狀況下,利用兩個零件、移動兩次,多半都可以抵達目標阻抗,但在某些情況下,如果用兩個零件時,中間那個點可能會離目標阻抗很遠,這時候就代表電路中會有一個很特異的特性阻抗存在中間,這時我們可能需要三個零件、移動三次,才可以比較好地抵達目標阻抗,而不會讓中間那個點偏離太遠。
利用兩個零件做阻抗匹配的電路,稱爲 L 型匹配電路,因爲一個串聯、一個並聯的電路,看起來就是個 L 型,而利用三個零件做阻抗匹配的電路,通常是並聯、串聯、並聯,看起來像個希臘字母 𝜋,因此稱之爲 𝜋 型匹配電路。
小結 #
這一回我們示範了一個實際的阻抗匹配計算,但因爲我們使用的 Smith Chart 刻度不夠細,只有到 0.1,爲了方便計算,我們將正規化阻抗從 Z = 0.78 + j0.12 四捨五入到 Z = 0.8 + j0.1,這種情況在使用紙本的 Smith Chart 做計算時常常發生,也會限制我們計算的精確度。
還好現在我們有許多電子化的 Smith Chart 工具,可以不必受到 Smith Chart 的印刷精度限制。下一回,我們要來介紹如何用這些電子化的 Smith Chart 來做更精確的阻抗匹配計算。
(責任編輯:賴佩萱)


