作者:Bird
上一回【Maker電子學】淺談高頻系統的原理與設計—PART12 中,我們利用 Microstrip Impedance Calculator 這個計算工具示範了 PCB 上 microstrip 傳輸線的特性阻抗計算,也說明了 PCB 製造上的一些參數。
這一回我們要進入另一個稍微複雜一點的領域,來聊聊阻抗匹配。
爲什麼要匹配? #
我們在剛開始談交流電路時,有提過訊號源阻抗與負載阻抗這兩件事,我們也說過,當訊號源的阻抗與負載的阻抗相同時,從訊號源傳送到負載的功率是最大的。今天我們要仔細來看一下這件事。
首先我們先用比較簡單的純電阻模型來推導。假設有一個訊號源,它的電壓是 VS,輸出阻抗是 RS,經過導線要將訊號傳輸到負載 RL,畫成電路圖就是這樣:
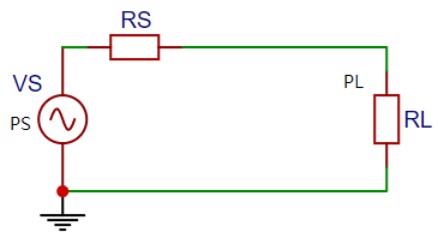
(圖片來源:Bird 提供)
根據歐姆定律,RL 上的功率等於 RL 乘上流過 RL 電流的平方:PL = I2RL,而流過 RL 的電流則由訊號源電壓 VS 與串聯的訊號源阻抗 RS 和負載阻抗 RL 決定,一樣遵循歐姆定律 V = IR:
I = V / R = VS / (RS + RL)
將電流 I 代回計算功率的式子,我們就會得到:PL = I2RL =(VS2/(RS + RL)2)RL,由於我們想要知道訊號源阻抗與負載阻之間的差異對功率傳輸的影響,我們先定義 k 爲訊號源阻抗與負載阻的比例:k = RL / RS
然後定義訊號源的輸出功率 RS 爲 RS = VS2 / RS,將這個兩個定義代進去計算功率,經過整理後會得到一個看起來比較簡潔的式子:RL = k /(k + 1)2⋅ PS,於是我們就得到訊號源功率與負載收到的功率之間的關係:它只和訊號源阻抗和負載阻抗之間的比例 k 有關。
從上面的式子似乎很難看出來 k 到底大比較好,還是小比較好。沒關係,我們直接開個試算表來畫圖看看。
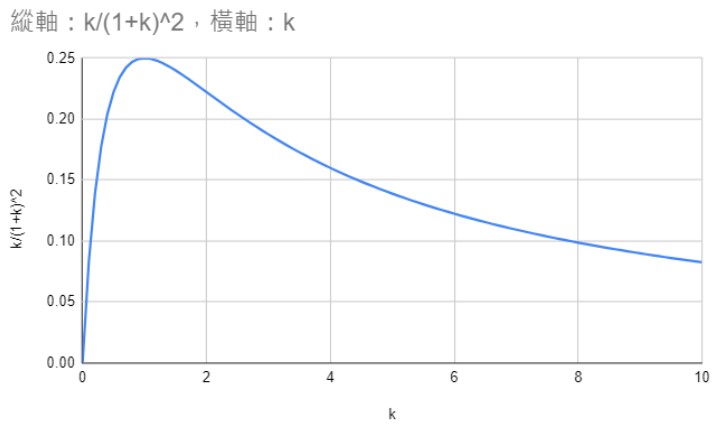
(圖片來源:Bird 提供)
從這張圖可以發現一個很妙的現象,當 k=1 時,k /(k + 1)2 的值最大,表示有最多的功率從 PS 傳送到 PL,但即使是最大,也只有 0.25;換句話說,即使是在負載阻抗與訊號源阻抗匹配的狀況下,也只有四分之一的能量可以從訊號源傳送到負載。如果阻抗不匹配、不相等時,能傳送過去的能量就更低了。
咦,即使是匹配時也只有四分之一的能量可以穿過去,那剩下四分之三哪裡去了?其實是被訊號源自己的阻抗給吃掉了。對,沒錯,RS 其實也會消耗能量。
複數阻抗 #
接下來我們要來看阻抗不是純電阻的情況。我們在聊交流電路時,有講過用來表示阻抗的的複數符號系統:用實部來代表電阻、用虛部來代表電抗。
Z = R + j X
如果電抗是電感性的,虛數那一項就是正的;如果電抗是電容性的,虛數那一項就是負的。我們把剛剛的電路再重畫一下,將純電阻的符號改爲複數阻抗 Z:
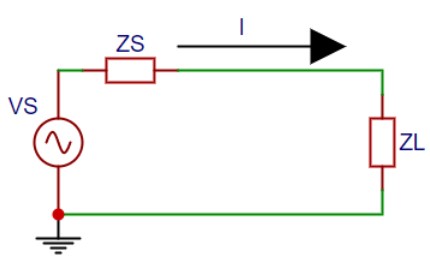
(圖片來源:Bird 提供)
用同樣的方式,我們可以計算整個系統的電流 I:I = V / Z = V / (ZS + ZL)= V / ((RS + RL) + j(XS + XL))
上面那個式子是複數的計算式,我們之前用圖片表示過它的定義:
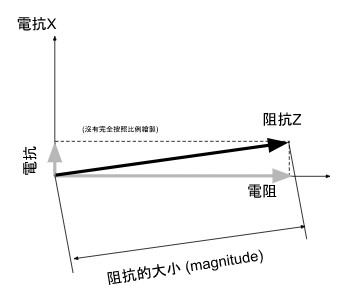
(圖片來源:Bird 提供)
由於我們現在只在意電流的大小,不在意它的相位,我們可以先取出阻抗的大小(magnitude),再用這個大小與訊號源電壓來計算電流的大小。
阻抗的的大小是:Zmag = SQRT((RS + RL)2+ j(XS + XL)2)
電流的大小就是 I = VS/ Zmag;功率就是 P =I2RL=RVS2/((RS + RL)2+(XS + XL)2 )
跟純電阻的公式很類似,如果要讓功率最大化,上面那個式子的分母就要最小化。
而由於分母兩項都是平方,因此值一定大於等於零,不可能是負的。第一項是阻抗中的電阻,它只能盡量小,但沒辦法爲 0;不過第二項是電抗,兩者的和就有可能爲 0。
在什麼情況下 XS + XL 會是 0 呢?就是當兩者大小相同、符號相反時,也就是說一個是電感性(符號爲正)另一個是電容性 (符號爲負)時:
XS + XL =0
XS=- XL
於是我們就得到了在複數阻抗時,傳送功率要最大的條件:
RS=RL
XS=- XL
在數學上,如果有兩個複數,它們的實部相同,虛部符號相反,就稱之爲「共軛複數」(conjugate complex);比照這樣大的定義,如果一個阻抗是 R + jX,那麼 R – jX 就稱之爲它的「共軛阻抗」。
而經由上面的推導,我們發現在複數阻抗中,如果要讓功率的傳送最大化,訊號源阻抗與負載阻抗必須要是共軛阻抗的關係;如果訊號源阻抗是 R + jX,我們就要設法讓負載的阻抗是 R – jX,這樣就可以讓傳送到負載的能量(或功率)最大化。
但是要怎麼樣讓負載的阻抗是 R – jX 呢?下回分解。
小結 #
我們這次用能量傳遞的觀點,看了阻抗匹配的重要性。我們先用純電阻模型的推導,得出在訊號源阻抗與負載阻抗相同時,能量傳遞會最大化這樣的結論,接著再把這個推導擴展到複數阻抗的環境下,得到複數阻抗要匹配時,其實是要兩個阻抗互爲共軛阻抗這樣的結論。
下一回,我們就要來看看,當負載阻抗不是目標的共軛阻抗時,我們有什麼方法可以將它變成共軛阻抗。
(責任編輯:賴佩萱)


