作者:Bird
上一回【Maker 電子學】GPS 接收器的原理與應用—PART2,我們解釋了 GPS 用的「展頻通訊」技術是怎麼一回事,並說明爲什麼所有的 GPS 衛星都可以用同一個頻率、同一個頻道傳送訊號,而地面的接收機又是怎麼把訊號解出來的,我們還說明了展頻通訊用的核心:虛擬隨機碼(PRN)具有的數學特性。
這一次我們要來看看 GPS 如何利用 PRN 的這些特性,達成定位的功能。
相關、相關 #
上次解釋了 GPS 用的 PRN 具有兩個數學性質:
每一個衛星的 PRN 與其它衛星的隨機碼逐一相乘再相加後,結果都接近 0,只有跟自己逐一相乘再相加後結果才不會是 0,這個特性稱為「低度互相關」,在線性代數上還有另外一個詞形容這個特性,叫做「正交」(orthogonal)。
每一個衛星的 PRN 只有跟自己完美對齊時,逐一相乘再相加後,結果才不會是 0,如果跟同一個 PRN,但是在時間上錯開,逐一相乘再相加後,結果都接近 0,這個特性叫「除了零延遲外低度自相關」。
「相關」這個詞在這裡的英文是「correlation」。我們之前一直在講的「逐一相乘再相加」這個解碼的動作,其實就是在確定兩個訊號之間的相關性,因此這個動作在數學上也叫做 correlation,而在接收器中用來執行這個動作的電路就稱爲 correlator。自己和別的 PRN 做 correlation 稱作「cross-correlation」;自己和自己做 correlation 稱作「auto-correlation」。
Correlation 這個計算很容易和微積分上的另一個函數計算「卷積」(convolution)搞混。兩者的計算方式很類似,都是將兩個函數或是訊號逐點相乘後再相加,但 correlation 是讓兩個函數從同一個方向開始逐點相乘後再相加,而 convolution 則是兩個函數一頭一尾逐點相乘後再相加,方向相反。
雖然兩者有很多類似的特性,但在通訊上我們比較常用 correlation 而不用 convolution,主要是因爲要計算 convolution 的話需要等到兩個訊號都到齊了,才能開始計算;而計算 correlation 則可以打帶跑:訊號一邊進來,不用等它全部收完,就可以開始一邊做 correlation、一邊等剩下的訊號進來。
第一個特性「與其它 PRN 的低度互相關」使 GPS 可以讓所有的衛星用同一個頻率 1575.42 MHz 向地面傳送訊號,地面的接收機也只需要接收一個頻率的訊號,就可以同時解出許多顆衛星的訊號。
第二個特性,跟 GPS 的定位原理有關。我們先來看看 GPS 是怎麼定位的。
定位原理 #
GPS 所使用的定位原理是「測距定位」。假設在一個平面上有一個點的位置是已知的,而我們知道我們與這個點的距離,那我們一定在以這個點爲圓心、距離爲半徑所畫出來的一個圓上。
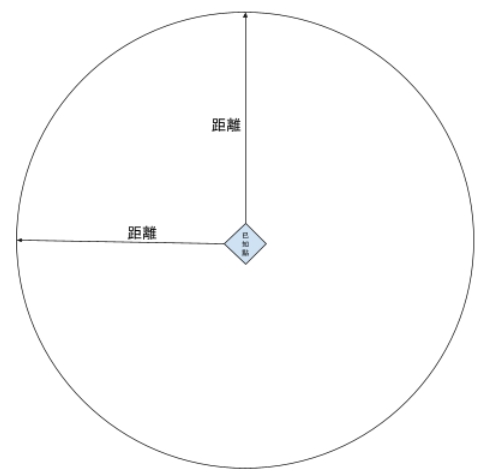
(圖片來源:Bird 提供)
如果這時有第二個已知點,我們也知道與這個已知點的距離,這時我們所在的位置,範圍就縮小到這兩個圓相交的兩個點上了。
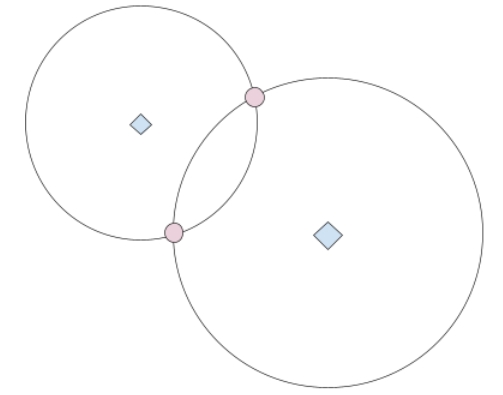
(圖片來源:Bird 提供)
以上是在平面上的例子。如果是在立體的三度空間中,情況會變得稍微複雜一點。
在立體空間中,如果我們知道與一個已知點的距離,那麼我們就可能位於以這個點爲圓心、已知距離爲半徑所畫出來的一個球體上。
如果這時有第二個已知點與第二個距離,那麼我們所在的位置,範圍就縮小到兩個球體所相交的所有點上,而兩個球體在立體空間中相交的形狀是一個圓形,因此我們可能位於這個圓形上的任何一點。
再進一步,如果這時還有第三個已知點與第三個距離,根據上面的推論,範圍就縮小到三個球體所相交的所有點上,或是在第二步驟中那個圓形與第三個球體所相交的點上。在空間中,一個圓形與一個球體相交的點有兩種狀況:大部分時候都是兩個點,只有當圓形與球體相切時,才會剩下一個點。
因此,藉由三個已知點的位置、三個與已知點的距離測量,就將我們在空間中的位置範圍縮小到之剩兩個點了。
聰明的讀者應該已經猜到,三個已知點可以是 GPS 衛星。當衛星的位置已知,而我們又可以測量我們到每一顆衛星的距離時,定位的範圍就剩下兩個點了,而這兩個點,一個位於地表,一個位於太空中,我們可以輕易地從座標的合理性判斷哪一個點才是我們所在的位置。
因此,現在的問題變成,我們要如何測量我們與衛星的距離。
測距碼 #
每一顆 GPS 衛星上都有一個很精確的原子鐘,而我們手上的接收器裡也有一個沒那麼準確但是精度也不差的時鐘,兩者在可能的範圍內盡可能的同步。
GPS 衛星會照著一組與時間有關的規則,不斷送出利用 PRN 編碼過的訊號,往地表傳送,而接收器這邊除了有時鐘外,也知道一樣的規則,知道在什麼時間送出來的 PRN 應該長什麼樣子。
衛星送出來的無線電訊號經過兩萬公里的跋涉,來到地表,需要一點時間,因此接收器收到訊號的時間與衛星發射的時間會有一點點差距。
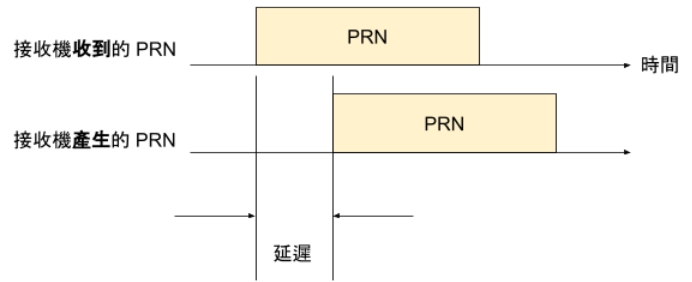
(圖片來源:Bird 提供)
這個延遲是由於無線電傳遞造成的。無線電雖然以光速行進,但要走過兩萬公里左右的距離也是需要一點時間的,如果衛星在你的頭頂,這是衛星距離接收機最近的狀況,來自衛星的訊號大概需要 67 ms 到達地表,如果衛星的仰角很低,接近地平線的話,與地表接收機的相對距離會稍微遠一點,來自衛星的訊號大概需要 85 ms 左右的時間到達接收機。
對於現在的數位電路來說,數十 ms 的時間其實已經很長,可以精確的測量了,至於要怎麼測量,就要用到 PRN 碼的第二個相關性了。
第二個相關性是「除了零延遲外低度自相關」,因此我們只要在接收機上產生一樣的 PRN,然後調整不同的延遲,再逐一跟接收到的訊號做 correlation。
比方說,我們可以在接收機上產生某一顆衛星的 PRN,然後將它延遲 65 ms、66 ms、67 ms… 等不同的時間,然後將接收到的衛星訊號跟延遲過的訊號逐一的做 correlation。
由於 GPS 的 PRN 之有在零延遲時的 correlation 才是正的,其它延遲時算出來都會是很小很小接近零的數字,因此在這個搜尋的過程當中,只會有一個延遲的時間,讓 correlator 的輸出有數字,其它的延遲造成的輸出都會是接近 0 的數字,而這個讓 correlator 有輸出的延遲,就是這組 PRN 從衛星傳遞到接收機所需要得時間。
這個延遲乘上光速,就是接收機到這一顆衛星的距離。
GPS 在 L1 波段上發送的這組 PRN 稱之爲 C/A 碼,C/A 是「coarse/acquisition」的意思,它是比較粗略(coarse)的定位用測距碼,定位精度較低,同時也可以用來在毫無線索的情況下尋找並捕獲(acquisition)衛星。
C/A 碼的 PRN 長度是 1023 個 bit,每組 PRN 的長度是 1 ms,因此 PRN 中的每個 bit 長度就是
1 ms /1023 = 0.977 us = 977 ns
在用 correlator 尋找最佳延遲時,我們每次移動 PRN 的單位就是一個 bit,你沒辦法叫 correlator 計算半個 bit 或 1/4 bit 移位的 correlation,因此每一個 bit 的時間長度就決定了測距的解析度。我們每一次最小只能移動 977 ns,因此算出來的距離每一個 step 就是光速乘上這個時間:2.9979 * 10^8(m/s)* 977 ns = 292 m
這就是 GPS 在 L1 頻段上的測距精度。這只是測距精度,不是定位精度喔。
理論上我們只要有三顆衛星的測距資訊,就能用前面講過的方法來定位,不過最後我們還剩下一個難題:時鐘的精度。
原子鐘與石英鐘 #
GPS 上用來計時的的是造價百萬美金以上的原子鐘,但我們的接收器上能用來計時的裝置頂多就是幾個 ppm 的石英振盪器,這兩者之間的精度相差了千萬倍以上。我們要如何讓接收器上的石英鐘 GPS 衛星上的原子鐘同步,好讓接收器準確知道衛星開始發送每一組 PRN 的時間呢?
這時候就需要用到第四顆衛星了。
衛星上的原子鐘雖然各自爲政,但在發射前都經過嚴格的校正,因此我們可以假設每一顆衛星上的原子鐘,報出來的時間都是一樣的。現在的問題是接收機上的石英鐘,時間可能不準,與 GPS 上的原子鐘有一個差距 Δt,但好消息是,由於每顆衛星上的時鐘是同步的,所以不管你接收哪一顆衛星,這個 Δt 都是一樣的。
於是我們的延遲測量問題就變成這樣了:
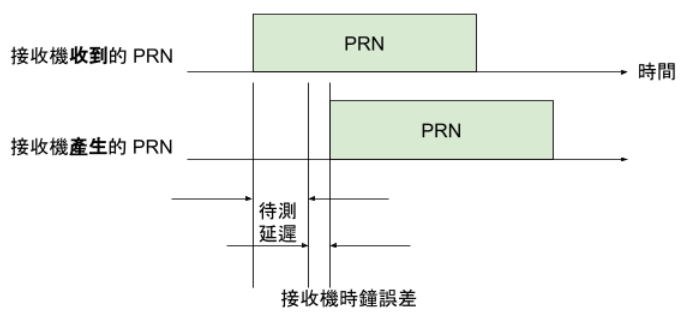
(圖片來源:Bird 提供)
要解幾個未知數,就需要至少幾個方程式。除了與衛星的距離是未知數之外,現在多了一個接收機的時鐘誤差也是未知數,因此我們需要多接收一顆衛星的訊號來解這個未知數。
這也就是爲什麼 GPS 至少需要收到四顆衛星的訊號才能定位的主要原因。
不過上面這樣的說明跟充滿考驗的現實世界還是有一點差距。GPS 的無線電訊號並不是完全在真空中傳遞,它離開衛星之後要穿越地球的大氣層才能到達地表,而大氣層中又有一層對無線電訊號不太友善的電離層,訊號穿過這些艱難險阻到達地面的過程,都會增加未知的延遲,影響定位精確度。
不像接收機時鐘誤差是對每顆衛星來說都一致,這些傳遞延遲會隨著衛星的仰角、高度、軌道位置甚至天氣而改變,每顆衛星都不一樣,因此我們需要更多的方程式來解更多的未知數。
這也就是爲什麼接收到的 GPS 衛星數量越多,定位精度就越高的原因。
小結 #
這一回我們介紹了 GPS 衛星利用測距來定位的原理,也說明了如何利用 PRN 的「除了零延遲外低度自相關」特性,用無線電訊號做距離測量。
了解了 GPS 的定位原理後,下一回我們要來看看實際的 GPS 接收器如何運作。
(責任編輯:賴佩萱)


