作者:Bird
上一回 【Maker電子學】淺談高頻系統的原理與設計 — PART15:史密斯圖(1),我們介紹了高頻電路設計中很重要的史密斯圖 Smith Chart,並說明了在圖上標註特定的特性阻抗的方式,以及它的物理意義。
這一回我們要來看看,如何利用史密斯圖估算元件數值,來設計阻抗匹配的電路。
在史密斯圖上移動 #
Smith Chart 上的點,都代表一個特性阻抗。我們說明 Smith Chart 時,使用的是經過「正規化」(normalized)的版本,因此不管你是用來計算特性阻抗 50 ohm 的 RF 系統、75 ohm 的有線電視系統,抑或是 45 ohm 的 USB 系統,都可以用同一張 Smith Chart。
圖的圓心代表的正規化特性阻抗是 Z = 1+j0,也就是我們的目標特性阻抗;純電阻、沒有感抗或容抗,是最匹配的阻抗。圖中的點離圓心的距離,就是反射係數:離開圓心越遠,反射係數越大、阻抗越不匹配;離圓心越近,反射係數越小,阻抗越匹配。
假設我們現在有一個 RF 晶片的輸出接腳,特性阻抗是 Z = 0.78 + j0.72,我們想加上一些像前兩回提到的那些神祕的電路,讓它的特性阻抗變成 Z = 1 + 0j,該怎麼做呢?

(圖片來源:Bird 提供)
如果在 Smith Chart 上把 Z = 0.78 + j0.72 這個點畫出來,我們可以看到它距離目標阻抗的距離:
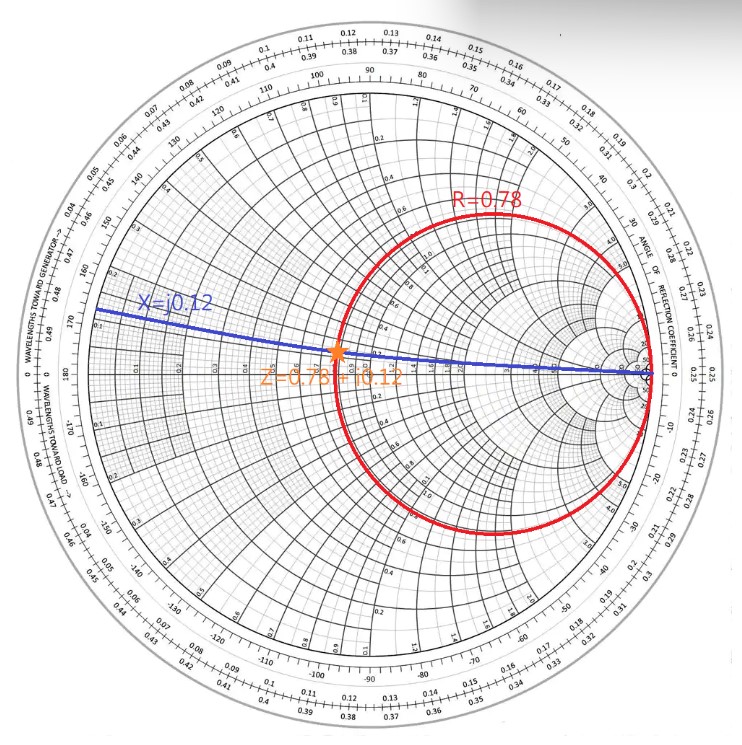
(圖片來源:Bird 提供)
現在的問題就是,要加上什麼零件,讓它朝著目標阻抗前進,直到到達目標阻抗呢?
顛倒世界 #
在說明使用 Smith Chart 來計算所需的零件之前,有個觀念要先介紹:導與抗。
我們之前在介紹特性阻抗時,所使用的物理量是電阻和電抗:電阻是計算式中的實部,由純電阻所產生,只會是正的;電抗是計算式中的虛部,由電感或電容產生,它可以是正的(電感性)、也可以是負的(電容性)。
電阻與電抗的物理量代表的都是對於能量傳遞的「阻礙」,因此這兩個物理量越大,對於能量傳遞的阻擋力量就越大。
如果我們定義一個反過來的物理量呢?比方說,我們定義一個物理量,它的意義是對於能量傳遞的「通過能力」。這個物理量越大,就代表讓能量通過的能力越好;越小,就代表讓能量通過的能力越差,也就是阻力越大。
在基本電學的世界,還真的有這樣的物理量,只是我們很少用到而已。它們就有點像電阻與電抗在另一個世界的孿生兄弟:電阻在顛倒世界裡的物理量叫做「電導」(conductance),它的定義就是電阻的倒數,慣用符號是 G:
電導 conductance G = 1 / R
而電抗在顛倒世界裡的物理量叫做「電納」(susceptance),它的定義就是電抗的倒數,慣用符號是 B:
電納 susceptance B = 1 / X
至於電阻與電抗加起來的阻抗,也有相反世界中的版本,它就叫「導納」(很合理的名字吧…),定義是阻抗的倒數,慣用符號是 Y:
導納 admittance Y = 1 / Z
整理一下:

(圖片來源:Bird 提供)
電導及電納的單位是「西門子」,這個單位是爲了紀念德國電學家 Ernst Werner von Siemens(1816-1892)。在 1971 年國際度量衡局正式承認爲電導及電納的標準單位之前,慣用的單位是「姆歐」(mho),這個字就是把歐姆的英文拼法倒過來,而如果要寫希臘字母的話,就是把歐姆慣用的 Ω 這個字母上下倒過來(但其實 24 個希臘字母中並沒有這一個)。
爲什麼要另外定義電導及電納這樣的物理量呢?其實主要跟計算的方便性有關。
我們知道,電阻串聯時,就將串聯的電阻值加起來就好了:R = R1 + R2
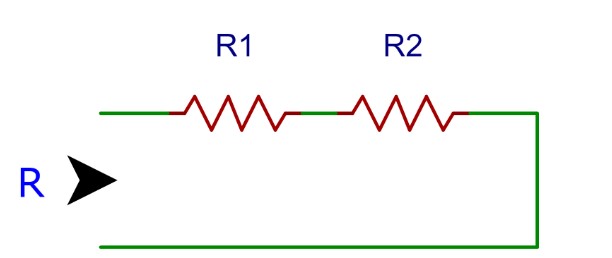
(圖片來源:Bird 提供)
但並聯時就麻煩了,得要將兩個電阻各取倒數,相加之後,再取倒數:R = 1 / (( 1 / R1)+(1 / R2))
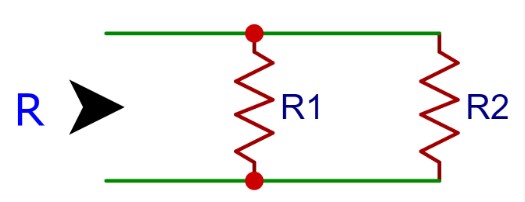
(圖片來源:Bird 提供)
我們將上面那個式子整理一下,把左邊的 R 也取倒數,就變成:1 / R =(1 / R1)+(1 / R2)
電阻的倒數不就是電導嗎?把 G = 1 / R 代入上面那個式子,就變成:G = G1 + G2
看起來是不是舒服多了?這就是電導與電納在計算式中爲我們帶來的方便性:串聯的結果就是電路中所有的電阻與電抗相加;並聯的結果就是電路中所有的電導與電納相加。
Smith Chart 的顛倒世界 #
既然 Smith Chart 是用來計算阻抗的,它一定也有顛倒世界的版本,可以用來計算電導與電納。沒錯,在顛倒世界中的 Smith Chart 長這個樣子:
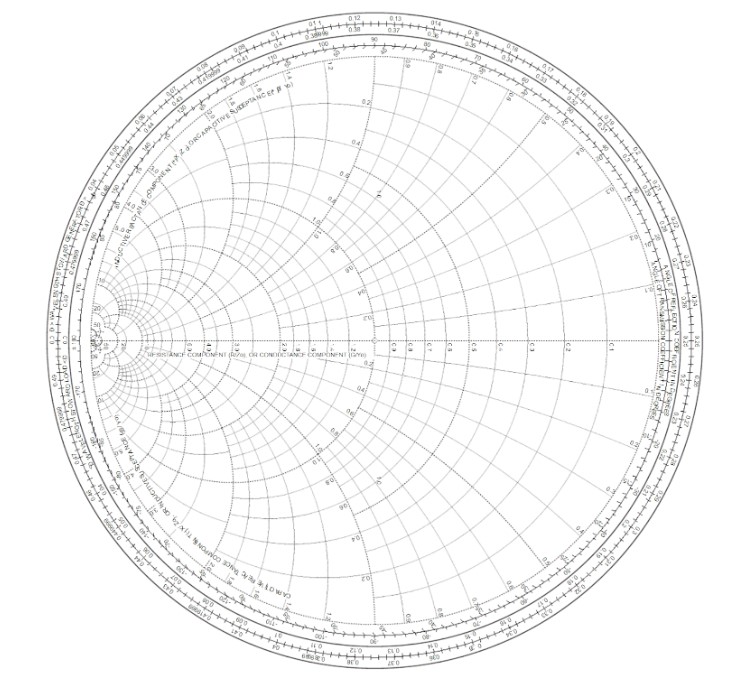
(圖片來源:Bird 提供)
乍看之下這張 Smith Chart 和我們原來用的 Smith Chart 沒什麼不同,但再仔細看,它是個左右相反的版本。原來那張 Smith Chart 密密麻麻的小圓圈是在圖的右半部,現在則到了左半部。
這張圖叫做 admittance Smith Chart,也就是導納版本的 Smith Chart。它的圓心一樣是 G = 1 + j0 的正規化目標阻抗,圖的上半部是電納爲正的電感性電納,而圖的下半部是電納爲負的電容性電納,圖中間的水平軸也是電納爲 0 的純電導位置;越往右去,電導越小(所以電阻就越大),直到圖的最右側,就是開路,也就是電導爲 0 的位置。
Admittance Smart chart 圖上的物理量位置和原來的 Smitch Chart 其實是一樣的,都是上半部是電感、下半部是電容;往右電阻大、往左電阻小,因此兩張圖其實可以重疊在一起畫,變成這個樣子:
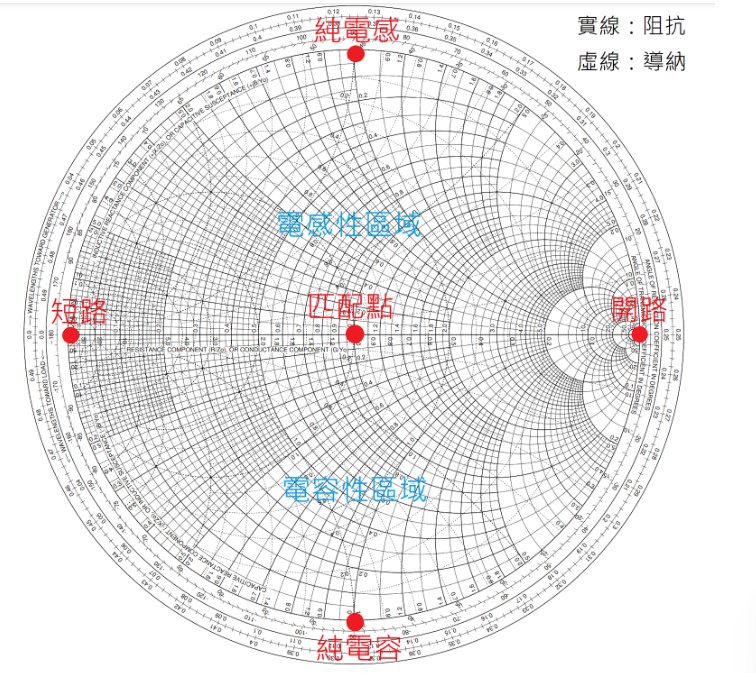
(圖片來源:Bird 提供)
這張圖叫做「Impedance and Admittance Smith Chart」,有時候也叫做「YZ Smith Chart」,因爲導納的符號是 Y、阻抗的符號是 Z。
由於阻抗與導納的兩張 Smith Chart 是完全重合的,想知道圖上的一個點代表的阻抗,只需要根據這個點的位置,查閱阻抗那張圖的軸線就可以得知,而如果想知道同一個點所代表的導納,只需要查閱導納圖的軸線就可以了(重疊的 Impedance and Admittance Smith Chart 讓我們可以方便地在阻抗與導納之間做轉換,這一點對於我們接下來的計算非常重要)。
設計阻抗匹配電路時,會用到電感與電容兩種元件、並聯與串聯兩種接法,排列組合之後,就會有四種電路:並聯電感、並聯電容、串聯電感、串聯電容。這四種電路在 Impedance and Admittance Smith Chart 上,各有各的路徑,巧妙的搭配這些元件和電路所造出來的路徑,就可以完成阻抗匹配的工作。
小結 #
這一回,我們介紹了與電阻與電抗相反的、在顛倒世界中的「電導」與「電納」物理量,並說明了利用電導與電納畫出來的 admittance Smith Chart,以及它與原版 Smith Chart之間的關係。
下一回,我們繼續介紹阻抗匹配電路在 Smith Chart 上形成的路徑,讓我們更接近阻抗匹配。
(責任編輯:賴佩萱)


