作者:實作派
講到三角函數大家一定很頭痛,加減乘除就已經夠煩了,為何還有人會發明三角函數這種東西?學三角函數到底要拿來幹嘛?日常生活中根本不會用到啊!這個推論非常合理,我沒有反諷的意思,我是真心覺得推論合理。
從 3D 繪圖說起
對中學生來說,電腦遊戲絕對是很有吸引力,如果你只是個玩家,基本上只要會打怪破關就可以了,甚至出國比賽得第一,這整個過程完全不需要三角函數,但如果你想做的事情與眾不同,你想寫一個軟體把一台 3D 戰機描繪在 2D 螢幕上,而且還要進一步作成動畫,那你非得需要三角函數不可。

把立體戰機畫在二維螢幕上(圖片來源:實作派提供)
因為描繪的過程中,你必須把立體戰機的三維(x,y,z)座標,轉換為二維的(x,y)才有辦法畫在平面的螢幕上,這個過程也可以稱為投影,這樣的轉換需要透過三角函數的計算才能完成。

利用 三角函數 才能把戰機投影到你看到的平面上(圖片來源:實作派提供)
不管多複雜的 3D 圖形,最終都會回歸到最基本的三角函數計算,我下面就來舉個簡單的例子。下圖是一個圓形運動的物體,這個物體好比戰機,右方的直線好比螢幕,我們眼睛看到的東西就是物體在右方直線上的投影量 sin(θ),這就是一個很簡單的三角函數應用,當你把它推廣到三維空間時,它就是我們講的 3D 運算。

圓形運動利用三角函數做成在 Y 軸的直線投影(圖片來源:實作派提供)
上面這個簡單的運算,就是一個基礎,它可以讓 3D 物體做投影以及旋轉,若要讓戰機畫在螢幕上,電腦必須在一秒鐘內計算 30 張甚至 60 張畫面,每個畫面要把飛機的每個座標算出來,當畫面中的物體越多、形狀越複雜、計算量就越大,這時你電腦的 CPU 可能會卡住,所以才有廠商發展了 3D 繪圖卡,它可以負擔很龐大的計算,讓 CPU 專心處理作業系統。
所以在動畫領域內,真正會用到三角函數的地方,就在這些動畫軟體、特效軟體、3D 繪圖卡裡面,所以如果只是玩遊戲,看動畫電影,壓根是不會用到三角函數,因為這群人是使用者不是開發者,他們不需要知道三角函數。
但是開發這些軟體的工程師們,他們是軟體的創造者,必須知道這一切的細節如何運作,當然也必須知道三角函數如何運用,所以各位可以思考一下,如果你想要開發繪圖卡,那你真的要好好把三角函數念好;如果你未來想要作電影特效,現在的套裝軟體很發達,不太需要算數學,你應該念應用美術之類的科系,除非你要開發新特效,如果美術與理科兩邊都念得很好,你將會是跨領域的人才。
遠距定位與測量
現在換個方式來看三角函數,其實它已經存在人類歷史超過上千年了,在電腦繪圖還沒有誕生之前,它們的任務就在於定位與丈量。以前當兵整隊時,有時為了隊伍的整齊劃一,總是會在地上標記號,這樣遠遠看起來就會非常整齊。
在地上標記號這件事情,就稱為定位,這種為了排隊整齊的需求,基本上用尺和繩子,就可以搞定,因為那是操場,又平又大很好定位,但如果現場地形高低起伏很大,這該怎麼辦呢?
舉個例子如下圖,假設今天要造一個高架橋,每隔一段距離 D 要做一個橋墩,目前已經做到 A 橋敦,即將要做 B 橋墩,你在現場該如何定出 B 的位置在哪裡?(B 點的橋墩基座,我先畫上去,實際上還沒有喔!)

要從 A 點定位 B 點的橋墩,需要一些方法(圖片來源:實作派提供)
從上面的圖看來,要找到 B 點似乎很容易,只要直接從 A 拉一條長度 D 的直線,不就找到 B 點了嗎?講都很容易,只是看圖畫線是一回事,現場要定位又是另外一回事,因為 A 與 B 中間隔了一座小山丘,施工人員在現場從 A 點根本看不到 B 點,你要如何在現場找到 B 點呢?
你有想過現場人員的感受嗎? 為了讓你身歷其境,我特別做了一張圖,讓你從施工人員的視角看現場。在寬廣的施工現場,你只會知道 B 點應該要在山丘的另一頭,但到底正確位置在哪裡,就有賴於精確的定位,位置搞錯高架橋就接不起來了。

從 A 點根本看不到 B 點,很難直接定位(圖片來源:實作派提供)
為了在現場能定位 B 點,我們必須繞道來定位,這時就需要用到三角函數了,因為在現場你能應用的資料就只有距離和角度而已,我們必須把地圖上的資訊轉換成角度與距離,方便現場定位。
實際要怎麼做呢?如下圖,A 點與 B 點在地圖上是已知的位置,我們必須在地圖找一個 C 點作為輔助點,這個 C 點在現場必須是可以同時看到 A 點以及大致上的 B 點,我們在地圖上利用三角函數把 θ1、L1、θ2、L2 算出來後,到了現場就可以依照這兩組角度與距離,由 A 點先定位 C 點,再由 C 點找到 B 點。
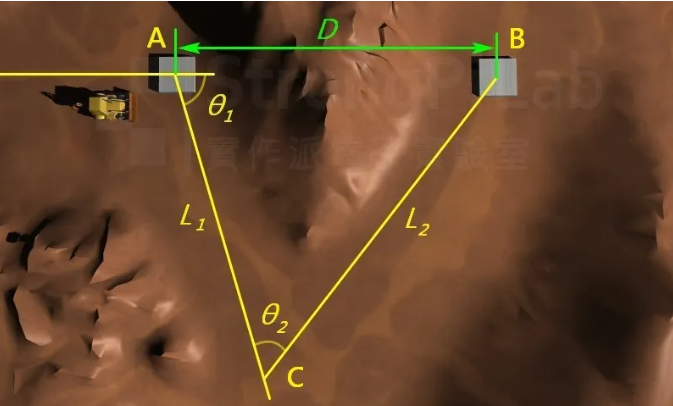
利用三角函數找到 B 點(圖片來源:實作派提供)
相信你很快就發現,照這樣說來三角函數似乎應用在工程上居多,沒錯!舉凡工程科系幾乎都會用到三角函數,電子學、電磁學、通訊原理、土木工程測量均屬此類。
但如果你立志學歷史、金融、語文,三角函數可說跟你幾乎沒關係,只是你多學一點也不會少一塊肉,而且可能還有加分效果,假如將來人家邀請你去當同步口譯,講的主題剛好是工程類別,若你曾經學過三角函數,翻譯起來當然就得心應手,即便你不是很會算它,但起碼翻譯得出來,下次這種專業的場合人家就會找你。
為了將來做準備
在國中高中這個階段,你可能學了一堆目前你認為永遠用不到的東西,三角函數、微積分,統計學,你也許會想,我的生活中從來不需要這些東西,從表象來看當然不需要,因為你是消費者!
舉個例子,使用手機、看電視節目,完全不需要三角函數,從事這些活動需要的是時間和金錢,人們總需要花錢買電視、買手機吧,有時甚至會買節目、買遊戲,你付出的金錢給了誰呢?就是給這些生產手機、電視與遊戲的工程師們,他們是生產者。
這些工程師們在人生的前半段花了很多時間歲月,學習他現在工作所需要的基礎知識,於是在他們人生的後半段才能有揮灑的空間。我們學習的東西越多,將來可以做的事情就越複雜,你的競爭力就高,人家就願意付比較高的代價來購買你的專業,於是金錢就從消費者流到生產者。
我這裡並不是說非得要學三角函數才叫作有專業,這取決於你將來想做什麼。如果你想當動畫師,你在藝術、色彩等方面就必須有一定的專業度,這也是需要時間培養,所以問題不在於我為何要學這個學那個,問題在於「我未來想做什麼?」,然後把現在的時間精力拿來為將來做準備,讓自己從消費者變成生產者。
如果你將來也想成為工程界的一員,請好好看待你正在學習的三角函數、微積分等,它們在將來會成為你非常好用的工具。
(本文經同意轉載自實作派電子實驗室、原文連結;責任編輯:賴佩萱)
- 【實作實驗室】分配器效能測試 - 2024/12/30
- 【實作實驗室】頻道功率怎麼測?有線電視頻譜長這樣! - 2024/12/12
- 【實作實驗室】無線滑鼠游標定格,電源開關更換 DIY - 2024/11/12
訂閱MakerPRO知識充電報
與40000位開發者一同掌握科技創新的技術資訊!



