作者:Bird
電源系統是電子電路中讓人又愛又恨的一部分,幾乎所有專案都少不了它,不管你的設計是插電、電池或是使用太陽能等其它更神奇的能量來源,你都需要電源系統來將能量轉換成適合使用的狀態(白話文:適當的電壓、電流)。
接下來的一系列文章,我想用盡可能淺顯易懂的方法,幫助讀者踏入電源設計的殿堂,而且,盡可能不用到太多的數學與計算。我們會先探討只能降壓的線性電源系統,接著再進入比較複雜、可以升壓、降壓,甚至產生負電壓的交換式電源系統。
這一回,讓我們先從歷史故事說起。
交直流大戰 #
看過電影「電流大戰」的人,應該都對當年愛迪生與奇異博士,啊不是,是特斯拉之間的直流交流系統之戰印象深刻。
愛迪生陣營所提倡的直流系統,從發電機出來就是直流電,一路經過輸配電系統後抵達用戶家中,用來點亮電燈泡、推動直流馬達驅使機械工作。
不過,直流系統最大的問題在於無法輕易改變系統電壓。當時雖然已經發明了變壓器,但變壓器只能在交流系統上運作,且那是個連真空管都還沒發明的年代,更不用說半導體開關元件,因此沒有適合的電路能將直流轉換成交流,再用變壓器改變電壓,所以當時的直流輸配電系統從發電機到用戶端的電壓都是一樣的,大約 100 V 左右的系統電壓就差不多在那個時候確立。
100 V 這樣的電壓對人體雖然有點危險,但以輸配電系統來說其實是很低的電壓。假設我們要輸送 10 KW 的能量到遠方,如果用 100 V 來傳輸,需要的電流就是:10000 (W) / 100 (V) = 100 (A)
如果整個輸送系統上有 0.01 Ω 的電阻,所造成的損耗就是:P =I2R= 100 * 100 * 0.01 = 100 (W),差不多是 1% 的損耗。
同樣輸送 10 KW 的能量,如果我們將電壓提升到 10,000 V,所需要的電流就變成:10000 (W) / 10000 (V) = 1 (A),而同樣 0.01 Ω 的電阻所造成的損耗就變成:P =I2R= 1 * 1 * 0.01 = 0.01 (W),電壓提升 100 倍,傳輸損耗變成萬分之一。
由於交流系統可以輕易用變壓器改變電壓,在輸配電時很容易將電壓升高,使得在同樣功率下的電流變小,降低損耗,所以愛迪生與特斯拉的直流交流系統大戰最後由交流系統勝出,主宰了接下來百年的輸配電系統。
變壓器 #
變壓器是這一波交直流大戰中的核心角色,它的電路圖符號大部分的人應該或多或少都有看過:
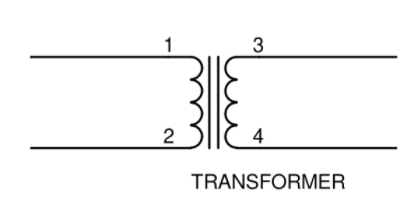
(圖片來源:Bird 提供)
它的電路圖符號同時也說明了它的結構和原理:兩個線圈,繞在同一個鐵芯上。
法拉第定律告訴我們,如果把一個電路放在變動的磁場中,會感應出一個電動勢,也就是電壓。因此如果我們在上圖的第一個線圈通上交流電,由於交流電會不斷變化,它會在這個鐵芯上造出一個不斷變化的磁場,而這個磁場就會在另一個線圈上感應出一個同樣不斷變化的交流電動勢。
一般來說,我們將輸入能量這一側的線圈稱爲一次測(primary)線圈,而輸出能量的另一測為二次測(secondary)線圈。輸入與輸出之間的電壓關係,是由變壓器上線圈的圈數所決定。原則上輸入與輸出的電壓比值,就是兩側線圈的圈數比值,比方說如果一次測繞了 100 圈、二次測繞了 20 圈,這個變壓器就會是一個降壓成 1/5 的變壓器,如果我們輸入 100 V 的交流在一次測,就會在二次測感應出 20 V、同樣頻率的交流電。
市面上可以買到一系列 110 V 輸入,低壓輸出的變壓器,它們的外形多半長這樣:

(圖片來源:Bird 提供)
其中一邊的接點會表示如 110 V、220 V 這樣的電壓,另一側則會有像是 6 V-0 V 或是 6 V-0 V-6 V 這樣的電壓,這個變壓器用電路圖符號畫起來是這樣:
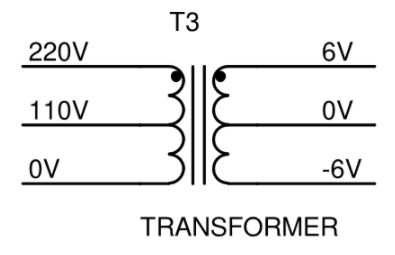
(圖片來源:Bird 提供)
大部分市售的變壓器,二次測如果有三個接點的話,都只印 6 V-0 V-6 V 這樣的標示,但是認真來說,其中一邊應該是負的,至於哪一邊是負的,哪一邊是正的,如果你不在意它與 110 V 交流電之間的相位關係的話,就不重要了,因爲在變壓器的世界中,所有的電壓都是相對的。
如果我們在變壓器的一次測 110 V 和 0 V 的接點上接上 110 V/60 Hz 的交流電,變壓器的二次側就會開始有輸出。如果我們把示波器的接地夾在二次測輸出的 0 V 端子上(千萬不要夾到一次測的任何端子,如果示波器沒做隔離的話會有很可怕的後果),並用探棒去看 6 V 和 -6 V 兩個端子的電壓,會看到這樣的輸出:
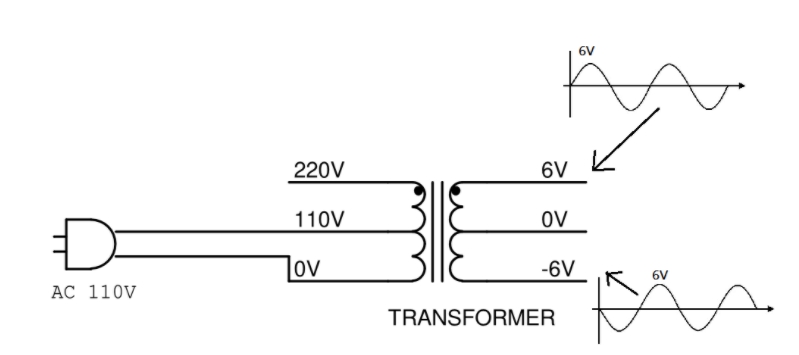
(圖片來源:Bird 提供)
在 +6 V 和 -6 V 的端子上,我們會看到兩個頻率一樣、相位相反的交流波形。
最簡單的電源電路 #
接下來我們來做一個最簡單的電路,把這個低壓的交流輸出轉變爲直流電(先別管 -6 V 那一組輸出,我們只用 +6 V 的輸出),我們要做兩件事:整流和濾波。所謂整流,是將方向不斷變換的交流電流,變爲只有一個方向流動的直流電流。這件事我們可以用二極體來達成:
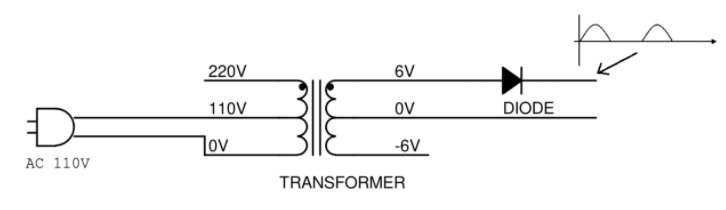
(圖片來源:Bird 提供)
利用二極體單向導通的特性,我們只讓電壓大於 0 的交流波形通過,而電壓小於 0 的部分就會被二極體攔下來。
我們得到了一個這樣的波形:
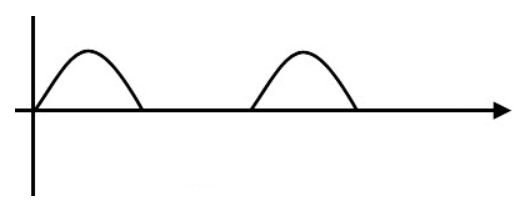
(圖片來源:Bird 提供)
它雖然長得有點醜,但定義上它仍然是「直流電」,因爲它的電壓始終大於 0,電流始終只往同一個方向流動,只是這是一個電壓一直變化的直流電,甚至有一半的時間電壓爲 0。
接下來我們要想辦法把這個個一直變化的波形「整」得漂亮一點,讓它不要一直變化。這個動作稱為「濾波」,可以用一顆電容器來達成:
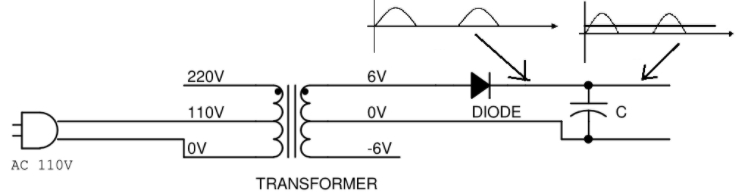
(圖片來源:Bird 提供)
在二極體的輸出與 0 V 端子之間接上一個電容器後,我們會得到一個平滑、不再變動的電壓了。電容器的作用就像一個水庫,當電路上的電壓高於電容器的端電壓時,電荷就流入電容器儲存起來;當電路上的電壓低於電容器的端電壓時,電荷就會向外流出電容器。
雖然我們得到了一個穩定的直流電壓,但這個電壓會比變壓器上標示的 6 V 要小蠻多的,原因是因爲我們用二極體整流時,砍掉了交流波形的負半週,因此有一半來自變壓器的能量沒有用到。
這時就輪到變壓器的另一個端子登場了。根據之前用示波器的觀察,+6 V 和 -6 V 這兩個端子的最高電壓相同,但相位相反;換句話說,當 +6 V 的端子進入電壓爲負值的負半週時,-6 V 端子的電壓會轉正。利用這個特性,我們可以加一顆二極體來把 -6 V 端子的正半週電流也拿來利用,變成這樣的電路:
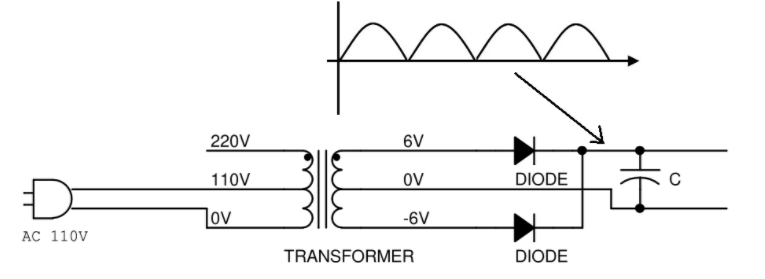
(圖片來源:Bird 提供)
由於這個電路同時利用到交流波形的正半週與負半週,它送往電容器的能量會是只用一顆二極體的兩倍,因此最後被電容器平滑出來的電壓也會是前一個電路的兩倍。
這個被電容器平滑之後電壓,稱之爲原來交流波形的 RMS(root-mean-square)電壓,也就是與原來交流波形等效、傳送一樣能量的直流波形電壓。至於爲什麼是用 RMS,而不是算術平均,是因爲能量與電壓的平方相關,它是一個二次項。
還記得微積分的讀者可能可以快速的算出 sin2𝞡 在一個週期內的積分爲 1/√2,差不多是 0.707,因此如果原來交流波形的峰值是 8 V,那麼整流、濾波出來的直流就是 8*0.707 = 5.6 V 左右。
事實上我們在標示交流電壓時,寫的都是 RMS 電壓,因此實際上的峰值電壓反而是 RMS 電壓的 √2 倍,差不多就是 1.414 倍。假設上面那個變壓器的輸出標示是 6 V,就表示我們用全波整流電路把它整流、濾波之後可以得到 6 V 的直流,而交流波形的峰值則是 8.484 V 左右。
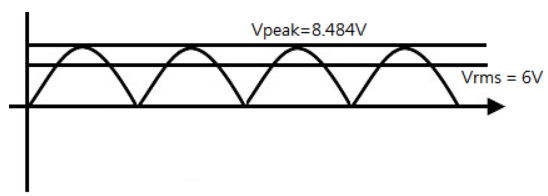
(圖片來源:Bird 提供)
而我們常說的 110 V 交流電壓,這個 110 V 指的也是 RMS 電壓,如果你實際去看 110 V 交流波形的峰值電壓,會發現它高達 155 V 左右。
利用全波整流電路與電容器濾波,我們得到了一個 6 V 的直流電壓,但如果你實際拿這個電壓當作電源使用,會發現一個問題:它並不是一個穩定的 6 V 電源。在沒有負載時,也許你可以有 6 V 的電壓,但隨著負載的增加、電流上升,這個 6 V 就不再穩定在 6 V,而會隨著電流上升而下降。
爲什麼會這樣?因爲這不是一個「穩壓」的電源。我們並沒有用額外的電路來控制它的輸出電壓,唯一決定它輸出電壓的因素就是變壓器的輸出線圈圈數(當然還有輸入的交流電壓)。變壓器的輸出能量來自於一次測線圈所產生的變動磁場,在輸出電流增加時它並不能無限制地提供能量,而會受到諸多限制如線圈本身的電阻、變壓器鐵芯的最大磁通量等因素。
雖然在一些很便宜的電子產品上偶爾還是會看到這樣的電源,但現今這種完全不做穩壓的電源設計已經越來越少見了。
小結 #
這一回我們從一個最簡單的 AC 降壓變壓器開始,說明了半波整流與全波整流電路,以及濾波之後的電壓計算,但這個電路並沒有穩壓的設計,它的輸出電壓會隨著輸出的電流變動。下一回我們就從線性穩壓電源開始,帶讀者一窺電源設計的世界。
(責任編輯:賴佩萱)



