作者:實作派
電力公司供電分為單相與三相,每個相之間可能會領先或落後,到底什麼是相位呢?相位的領先、落後又是怎麼回事?
認識家裡的交流電
你我家裡的交流電基本上長得和下面圖示一樣,上面紅色是 +110 V、下方藍色是 -110 V,誰正誰負不重要,重要的是一正一負,這樣就稱為單相。
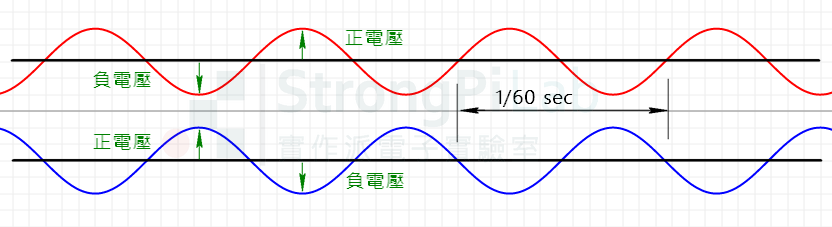
110 V line with 0 and 180 deg phase(圖片來源:實作派提供)
這時可能有人會說,這哪裡是單相?這兩條火線的波形差了 180 度,所以一個是 0 度,另一個是 180 度,有兩種角度應該稱為「雙相」吧!這樣的邏輯其實不能算錯,只是這個定義與實務上的定義不同;在實務上,電力系統所謂的單相,是指我們只用發電廠過來的三相電中的一個相位。
家庭用電之所以會有反相的情況,是因為變壓器接線的關係。如下圖,左右兩個變壓器都是一樣的規格 6.6 KV/220 V,若二側的 0 V 接在中間,則上下分別為 +110 V 與 -110 V,也就是一般市電的接法;若 0 V 接在最下方,則會得到 +220 V,這樣不管怎麼接它們都稱為單相電,因為左邊的 6.6 KV 是來自輸電線的其中一個相位。

single phase connection(圖片來源:實作派提供)
什麼是相位 Phase?
在英文裡面,phase 是指一件事情的階段,在波形的敘述上我們也用相位 phase 來敘述波形在某時間點的階段。大家最熟悉的應該就是正弦波,來回振盪一次在數學上的週期稱為 2π,也稱為 360 度,只是大家都習慣從 0 度開始畫弦波,然後結束於 360 度(或稱為下一個 0 度),但其實從任何角度開始畫弦波都可以,只要開始與結束是在同一個角度就行。
在工程上,我們經常用旋轉半徑的投影量來表示波形的動態,你可以用 sin 也可以用 cos 來做投影量,一般我習慣用 cos 來表示波形,由於波形會動所以我們會在角度的地方以角頻率乘以時間 ωt 來表示不斷前進的角度,至於波形的起始角度就以 θ 來表示,也稱為相位角,公式寫起來就像下面這個樣子,s(t)可以是電壓或電流。
s(t)=Acos(ωt+θ)
你可以想像有個長度為 A 的半徑,不斷地繞著原點旋轉,它的投影量就是這個s(t)波形,所以繞一圈剛好就是一個週期的 cos 波形,就像下圖一樣,雖然下圖只有標示起始相位,但你可以當作它是 t=0 時的位置,隨著時間移動,半徑便開始逆時針旋轉,至於圖中的座標軸,橫軸為實數、縱軸為虛數,為何會有虛數?這是因為我引用了歐拉公式,這個後面會談到,實際的波形則要看實軸上面的訊號變化。
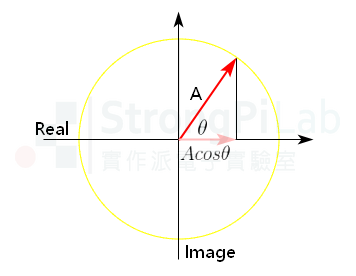
phasor of cosine waveform(圖片來源:實作派提供)
剛才我們有提到,其實繞一圈不見得要從 θ=0 開始,若你有 5 個頻率相同的波形,各自從不同的 θ 開始繞,你在時間軸上就會看到 5 個形狀一樣的波形,只是有些靠左邊一點,有些靠右邊一點,這些左右差距稱為相位差,如下圖所示。
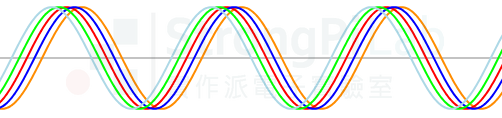
phase shift waveform(圖片來源:實作派提供)
雖然有相位差的波形在示波器上可以很明顯地看出波形之間的時間差距,但我們在討論相位差時,通常不會以時間差來討論,而是以「角度」來討論,因為相位角才是真正影響波形左右位移的主角。
相位領先 lead/相位落後 lag
接著我們實際畫出 2 個有相位差的波形,下圖是把剛才在複數平面的圓形順時針轉 90 度,這樣才好把波形橫著畫出來,你可以看到,圓周上兩個紅色與綠色的點,它們的投影量在左邊的垂直線上,就是直線運動的紅點與綠點,如果再沿著時間軸把投影量的位置一個個記錄起來,你就會看到波形,如下圖所示:

green wave leads red wave; red wave lags green wave(圖片來源:實作派提供)
所謂相位領先與落後是很直觀的,以黃色圓上的兩個點來說,綠點跑在前面,紅點跑在後面;若換成觀察它們左方的投影量,也就是直線上下運動的點,你也能明白看出綠點居於領先地位,紅點居於落後地位。
以上圖為例,很明顯的結論是,綠點領先紅點 90 度;反過來說,紅點落後綠點 90 度。也可以說成,綠色波形領先紅色波形 90 度、紅色波形落後綠色波形 90 度。
也許有人會說領先 90 度能否說成落後 270 度?由於位置是一樣的,因此答案是可以的,只是這樣的敘述很不直觀,也很難與別人溝通,所以大家都會挑比較近的角度來說明相位差;若把波形寫成數學式,落後相位的波形相位角為負數,領先相位的波形相位角為正數。
Sg(t)= Acos(ωt)— Green waveform
Sr(t)= Acos(ωt–90°)— Red waveform
相量(Phasor)圖
你應該會發現,使用三角函數來表達波形,很沒有親和力,要是多來幾個波形,那豈不是要算到昏倒?因此科學家們引進了複數平面的相量(phasor)圖的概念。原本的波形公式是這樣:
S1(t)= Acos(ωt+0°)
S2(t)= Acos(ωt+θ)
假設時間靜止 t=0,cos 裡面的角度只剩下相位角,那麼若以 S1 為基準,相位表示式將會是:
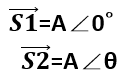
所以若在複數平面畫成圖的話,就是是下圖這個樣子。相量 S1 與 S2 的加減,完全就是向量運算,算完的結果只要投影在水平的實數軸上,就幾乎可以想像最後的波形了,這樣應該有比較很方便吧!基本上只要用畫的就能得到大概的答案,真的要算角度與長度的話再來動筆算。
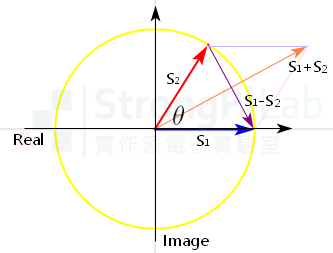
phasor(圖片來源:實作派提供)
只是訊號都是實數,那為何會冒出含虛數座標的複數平面呢?是的,我們的波形都是實數,之所以會採用複數,是為了幫助分析,並非表示虛數會出現在生活中,它只是數學上創造出來的東西,虛數在當時可能也沒想到會對工程上的分析有所幫助。
虛數能當作分析工具,這要歸功於 18 世紀的數學家兼工程師 Euler,他發現三角函數與複數之間的關係,可以用指數的複數次方來表示,也就是這個著名的 Euler formula:
ejθ=cosθ+jsinθ
所以任何一個弦波我們都能寫成:
s(t)
=A∠θ—相量式
=Aej(ωt+θ)—歐拉公式 Euler formula
=Acos(ωt+θ)+ jAsin(ωt+θ)—展開式
雖然我們要的東西只存在於實數,但為了分析導入 Euler 公式,把我們要的東西當作是旋轉半徑的實軸投影量,如此一來就能輕易畫出向量;若你有好幾個波形要相加,只需要將它們的向量全部加起來,就能知道最後波形的振福與相位角了。
只是不巧,相量(phasor)與向量 (vector)在中文上發音相同,所以很容易搞混,我只能說,phasor 一定是個 vector,但是 vector 不見得是個 phasor,至少在電力與通訊的領域中我是這樣理解的。
三相交流電
所謂三相交流電就是供電方式需要用到三個相位,因此需要三條電線,之所以會有三相是因為發電機組本身的物理結構就包含了三組線圈,每組線圈間隔 120 度,產生出來的電壓電流彼此也就相隔 120 度。
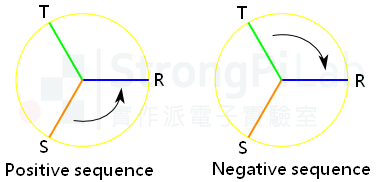
phase sequence(圖片來源:實作派提供)
三相電有相序 phase sequence 的分別,任兩條接反了馬達會反轉,不像一般家裡的單相電,正插反插電風扇都轉同一邊,所以相序很重要;一般相量圖逆時針旋轉時若依序到達 0 度,標示為 R-S-T 稱為正相序,R-T-S 稱為負相序。
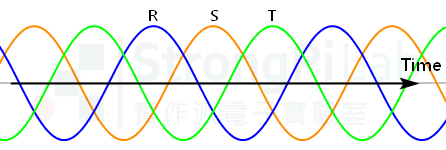
three phase waveform – positive sequence(圖片來源:實作派提供)
如果你不知道相序,可以用相序表來檢查,我曾經聽過有工廠的供電相序在停電後復電時,由於台電的相序接錯導致抽風機馬達反轉,而且噪音頗大,這樣很傷機器;如果你的機器很寶貴,禁不起一次的反轉,可以接上變相器,讓機具馬達的相位不會因此受變化。
- 【實作實驗室】分配器效能測試 - 2024/12/30
- 【實作實驗室】頻道功率怎麼測?有線電視頻譜長這樣! - 2024/12/12
- 【實作實驗室】無線滑鼠游標定格,電源開關更換 DIY - 2024/11/12
訂閱MakerPRO知識充電報
與40000位開發者一同掌握科技創新的技術資訊!



