【實作實驗室】認識音響與工程上常見的計量單位 — dB 分貝

Posted By StrongPiLab on 7 月 24, 2019 in 實作派StrongPiLab, 教學文 | 0 comments

作者：實作派 Lab

在音響的音量旋鈕上經常會看到 dB 這個字樣，而且最小的音量還會標示為負值，例如 -90 dB 之類的。為何音量標示不直接用 0~100 就好呢？而要使用一個看起來很不直覺的標示方式？本文將為各位解釋分貝（decibel/dB）是怎麼來的。

有感與無感的差別

如下圖，假設公司的加薪方式有 A 與 B 兩種，你會選哪一種呢？

A. 每月等距增加 1 萬元
B. 每月倍數增加 2 倍

我想大多數人會選擇 B，因為這種加薪幅度超有感；反觀 A，第二個月是第一個月的 2 倍，到了第六個月卻是前一個月的 1.2 倍，倍數縮小了因此越來越無感。

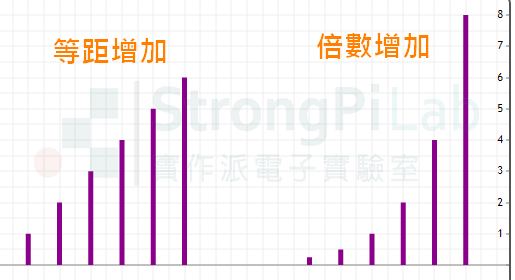
倍數增加較等距增加較有感（圖片來源：實作派提供）

自然界只對倍數有感

科學上有一種計量方式，可將倍數化為線性，經過轉換後，只要數字較大的值就表示真的「很大」，讓科學家較容易比大小。

這種轉換很類似人類的感官，這邊有兩個例子：

琴鍵上高兩個 8 度，耳朵只會覺得音調「等距」高了 2 階，但其實頻率已經變為 2²=4 倍
地震芮氏規模的每個量級之間，人們只覺得震度固定增加一階，但能量其實差了 32 倍

不知各位對於上列事情有無同感？這種將倍數化為線性的概念，就是分貝 dB 的原始構想。

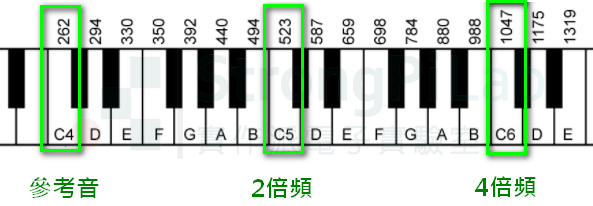
琴鍵上音高八度，耳朵察覺音調高了 2 階，但事實上頻率已差 4 倍（圖片來源：實作派提供）

認識 dB 分貝

在數學上唯一能將倍數化為線性的函數就是對數，例如 10 倍、100 倍、1000 倍可以分別轉換為 1、2、3 這樣簡單的數字，因此在工程上分貝的定義就是以 log 函數做轉換，因此有了下列的公式：

$A= 10 log\left ( \frac{P}{P_{ref}} \right ) dB$

（A 為 dB 數、P為功率、P_ref為參考功率）

以上的公式專門用來衡量「能量」的大小，這些量稱為 Power Quantity，若衡量的對象是電壓 V、電流 I、聲壓 SPL 之類的，這些屬於「場量」 Field Quantity，那麼公式前面的 10 會變成 20，：

$A= 20 log\left ( \frac{F}{F_{ref}} \right ) dB$

（A 為 dB 數，F 為場量，F_ref為參考場量）

我們把分貝的倍數列成表格大家就比較清楚了，基本上若能量比有 2 個零的話，dB 數就會是 2 開頭，以此類推，所以 dB 只要增加一點，實際的倍數可是會增加很多的喔！

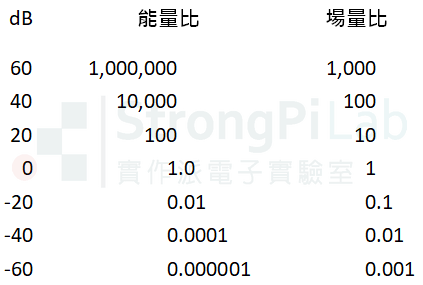
（圖片來源：實作派提供）

Log 前面為何有 10

利用 log 所得出的數值有個特別的單位稱為貝（B，Bel），但這個數值有點偏小，因此科學家才再弄一個十分之一 Bel 的單位，也就是分貝（dB，Decibel）。 dB 的公式便必須在 log 之前乘上 10，變成 1 B=10 dB。

Log 前面為何有 20

第二個公式裡的 20 是怎麼來的呢？由於 dB 是以能量（power）的觀點來出發的，若計量的數值是場（Field），例如電壓、電流，我們就得將它換成能量才能算 dB。

以電功率的例子而言，電壓 V 與電流 I 需要平方才會與功率同級數：

$power= \tfrac{V^{2}}{R}=I ^{2}R$

因此，

$A= 10log\left ( \frac{P}{P_{ref}} \right )= 10log\left ( \frac{F^{2}}{F_{ref}^{2}} \right )= 20log\left ( \frac{F}{F_{ref}} \right )$

再來看聲壓 sound pressure 的例子，聲壓 p 要平方之後才會與功率同級數：

$Sound Power= \frac{Ap^{2}}{\rho c}cos\theta$ （A=面積、p=聲壓、ρ=密度、c=速度）

所以場量的 dB 公式前面的 20 就是從平方演變過來的。

音量的 dB

根據上面的公式，我們知道 dB 是與某個基準 F_ref比較的倍數得來的，它是一個倍數的表示法，但用在音量測量上，是以多少來當作基準呢？音量的 dB 是以聲壓 20 μPa 為基準，這個聲壓據信是人可以聽到的最小聲音，因此 100 dB 的噪音，聲壓並不是 20 μPa 的 100 倍，而是 10 萬倍。